Question

If $\begin{vmatrix} x-4 & 2x & 2x \\ 2x & x-4 & 2x \\ 2x & 2x & x-4 \end{vmatrix} = (A + Bx)(x - A)^2$, then the ordered pair (A, B) is equal to

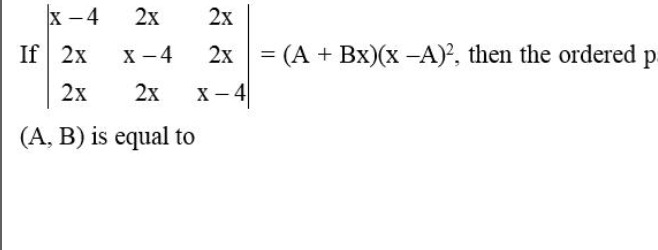
Answer 1

(-4, 5)

Answer 2

Solution:

Given the matrix

$$\begin{vmatrix} x-4 & 2x & 2x \\ 2x & x-4 & 2x \\ 2x & 2x & x-4 \end{vmatrix},$$

we recognize it has the form with diagonal entries $r = x-4$ and off-diagonals $s = 2x$. A standard formula for such a matrix is:

$$\det = (r-s)^2 \cdot (r+2s).$$

1. First, compute $r - s$:

   $$r-s = (x-4) - 2x = -x-4,$$

   so

   $$(r-s)^2 = (-x-4)^2 = (x+4)^2.$$

2. Next, compute $r+2s$:

   $$r+2s = (x-4) + 2(2x) = x-4+4x = 5x-4.$$

Thus, the determinant equals:

$$(x+4)^2 (5x-4).$$

We are given that

$$\det = (A + Bx)(x-A)^2.$$

By comparing, we identify:

• $(x-A)^2 = (x+4)^2$  ⟹  $A = -4$,
• $A+Bx = 5x-4$  ⟹  substituting $A = -4$ gives $-4 + Bx = 5x - 4$, so $B = 5$.

Answer: The ordered pair $(A, B) = (-4, 5)$.

---

Core Explanation:

• Use the formula for determinants of matrices with $r$ on diagonal and $s$ off-diagonals.
• Calculate $(r-s)^2 = (x+4)^2$ and $r+2s = 5x-4$.
• Equate with $(A+Bx)(x-A)^2$ to find $A = -4$ and $B = 5$.