Question

If

$\begin{vmatrix} a^2 & bc & ac+c^2 \\ a^2+ab & b^2 & ac \\ ab & b^2+bc & c^2 \end{vmatrix}$

= $ma^nb^nc^n$, then m + n =

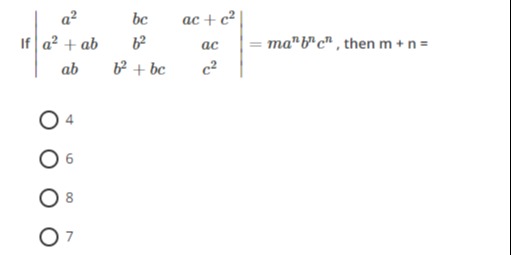
• A. 4
• B. 6
• C. 8
• D. 7

Answer 1

Answer: (B)

6

Answer 2

The given determinant is

$D = \begin{vmatrix} a^2 & bc & ac+c^2 \\ a^2+ab & b^2 & ac \\ ab & b^2+bc & c^2 \end{vmatrix}$

We can take out common factors from the columns. Take out $a$ from the first column, $b$ from the second column, and $c$ from the third column.

$D = abc \begin{vmatrix} a & c & a+c \\ a+b & b & a \\ b & b+c & c \end{vmatrix}$

Let $D' = \begin{vmatrix} a & c & a+c \\ a+b & b & a \\ b & b+c & c \end{vmatrix}$.

We can simplify this determinant using row or column operations. Apply the column operation $C_3 \to C_3 - C_1 - C_2$.

$D' = \begin{vmatrix} a & c & (a+c) - a - c \\ a+b & b & a - (a+b) - b \\ b & b+c & c - b - (b+c) \end{vmatrix} = \begin{vmatrix} a & c & 0 \\ a+b & b & -2b \\ b & b+c & -2b \end{vmatrix}$

Now, expand the determinant $D'$ along the first row:

$D' = a \begin{vmatrix} b & -2b \\ b+c & -2b \end{vmatrix} - c \begin{vmatrix} a+b & -2b \\ b & -2b \end{vmatrix} + 0 \begin{vmatrix} a+b & b \\ b & b+c \end{vmatrix}$

$D' = a [b(-2b) - (-2b)(b+c)] - c [(a+b)(-2b) - (-2b)b]$

$D' = a [-2b^2 + 2b(b+c)] - c [-2b(a+b) + 2b^2]$

$D' = a [-2b^2 + 2b^2 + 2bc] - c [-2ab - 2b^2 + 2b^2]$

$D' = a [2bc] - c [-2ab]$

$D' = 2abc + 2abc = 4abc$

Now substitute the value of $D'$ back into the expression for $D$:

$D = abc \cdot D' = abc \cdot (4abc) = 4a^2b^2c^2$.

The problem states that the determinant is equal to $ma^nb^nc^n$.

Comparing $4a^2b^2c^2$ with $ma^nb^nc^n$, we can identify the values of $m$ and $n$.

$m = 4$ and $n = 2$.

We are asked to find the value of $m+n$.

$m+n = 4+2 = 6$.