Solveeit Logo
Login

Question

Question: If $\begin{vmatrix} a & b & c \\ b & c & a \\ c & a & b \end{vmatrix}$ = k(a+b+c)($a^2 + b^2 + c^2$-...

If ∣abcbcacab∣\begin{vmatrix} a & b & c \\ b & c & a \\ c & a & b \end{vmatrix} = k(a+b+c)(a2+b2+c2a^2 + b^2 + c^2-bc - ca - ab), then k =

Answer

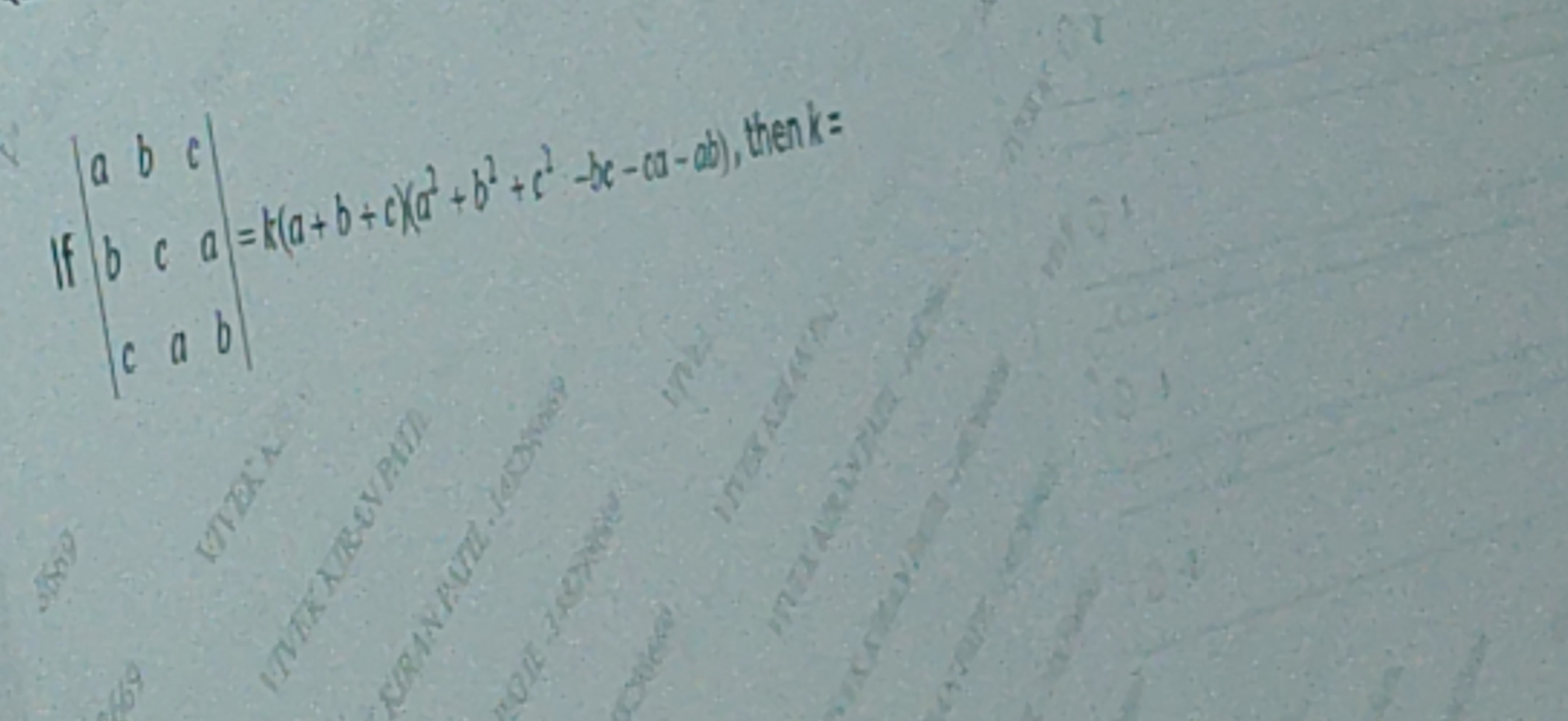
-1

Explanation

Solution

The given determinant is: D=∣abcbcacab∣D = \begin{vmatrix} a & b & c \\ b & c & a \\ c & a & b \end{vmatrix}

Step 1: Evaluate the determinant We expand the determinant along the first row: D=a(c⋅b−a⋅a)−b(b⋅b−c⋅a)+c(b⋅a−c⋅c)D = a(c \cdot b - a \cdot a) - b(b \cdot b - c \cdot a) + c(b \cdot a - c \cdot c) D=a(bc−a2)−b(b2−ac)+c(ab−c2)D = a(bc - a^2) - b(b^2 - ac) + c(ab - c^2) D=abc−a3−b3+abc+abc−c3D = abc - a^3 - b^3 + abc + abc - c^3 D=3abc−a3−b3−c3D = 3abc - a^3 - b^3 - c^3

We can rewrite this as: D=−(a3+b3+c3−3abc)D = -(a^3 + b^3 + c^3 - 3abc)

Step 2: Apply the algebraic identity We know the algebraic identity for the sum of cubes: a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ca)a^3 + b^3 + c^3 - 3abc = (a+b+c)(a^2 + b^2 + c^2 - ab - bc - ca)

Substitute this identity into the expression for D: D=−(a+b+c)(a2+b2+c2−ab−bc−ca)D = -(a+b+c)(a^2 + b^2 + c^2 - ab - bc - ca)

Step 3: Compare with the given expression The problem states that: D=k(a+b+c)(a2+b2+c2−bc−ca−ab)D = k(a+b+c)(a^2 + b^2 + c^2 - bc - ca - ab)

Comparing our derived expression for D with the given form: −(a+b+c)(a2+b2+c2−ab−bc−ca)=k(a+b+c)(a2+b2+c2−bc−ca−ab)-(a+b+c)(a^2 + b^2 + c^2 - ab - bc - ca) = k(a+b+c)(a^2 + b^2 + c^2 - bc - ca - ab)

By direct comparison of the terms, we can see that: k=−1k = -1

The value of k is -1.

The final answer is −1\boxed{-1}

Explanation of the solution: The determinant ∣abcbcacab∣\begin{vmatrix} a & b & c \\ b & c & a \\ c & a & b \end{vmatrix} evaluates to 3abc−(a3+b3+c3)3abc - (a^3 + b^3 + c^3). Using the algebraic identity a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ca)a^3 + b^3 + c^3 - 3abc = (a+b+c)(a^2 + b^2 + c^2 - ab - bc - ca), we can write the determinant as −(a+b+c)(a2+b2+c2−ab−bc−ca)-(a+b+c)(a^2 + b^2 + c^2 - ab - bc - ca). Comparing this with the given expression k(a+b+c)(a2+b2+c2−bc−ca−ab)k(a+b+c)(a^2 + b^2 + c^2 - bc - ca - ab), we find that $k = -1.