Question

If $|\bar{a}|=5$, $|\bar{b}|=3$, $|\bar{c}|=4$ and $\bar{a}$ is perpendicular to $\bar{b}$ and $\bar{c}$ such that angle between $\bar{b}$ and $\bar{c}$ is $\frac{5\pi}{6}$, then $[\bar{a}\ \bar{b}\ \bar{c}] =$

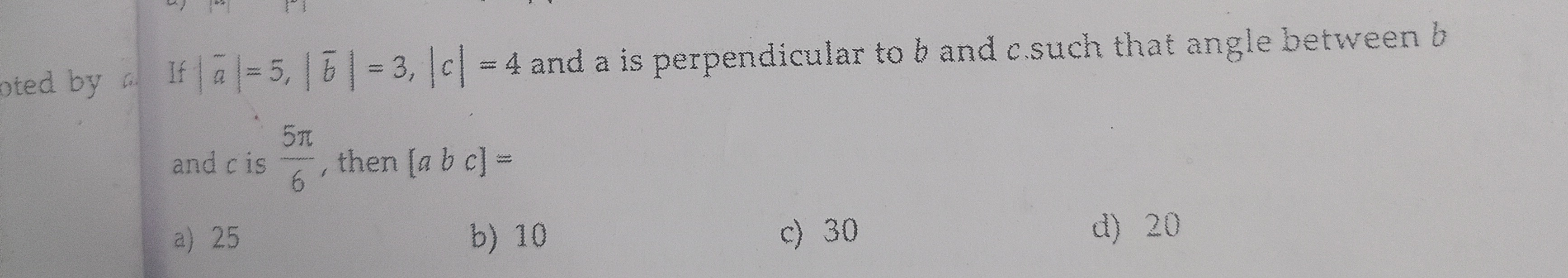
• A. 25
• B. 10
• C. 30
• D. 20

Answer 1

Answer: (C)

30

Answer 2

Since $\bar{a}$ is perpendicular to both $\bar{b}$ and $\bar{c}$, it is parallel (or anti-parallel) to $\bar{b} \times \bar{c}$. Thus,

$[\vec{a}\ \vec{b}\ \vec{c}] = \vec{a}\cdot (\vec{b}\times\vec{c}) = |\vec{a}|\;|\vec{b}\times\vec{c}|$

Now,

$|\vec{b}\times\vec{c}| = |\vec{b}|\;|\vec{c}|\sin\theta = 3\times4\times\sin\left(\frac{5\pi}{6}\right)$

Since $\sin\frac{5\pi}{6} = \sin\frac{\pi}{6} = \frac{1}{2}$,

$|\vec{b}\times\vec{c}| = 3\times4\times\frac{1}{2} = 6$.

Thus,

$[\vec{a}\ \vec{b}\ \vec{c}] = 5\times6 = 30$.