Question

If $|\bar{a}|=3$, $|\bar{b}|=5$ and $|\bar{c}|=7$ and $\bar{a}+\bar{b}+\bar{c}=0$ then the angle between $\bar{a}$ and $\bar{b}$ is

$\bar{a}+\bar{b}=-\bar{c}$ squaring on both sides

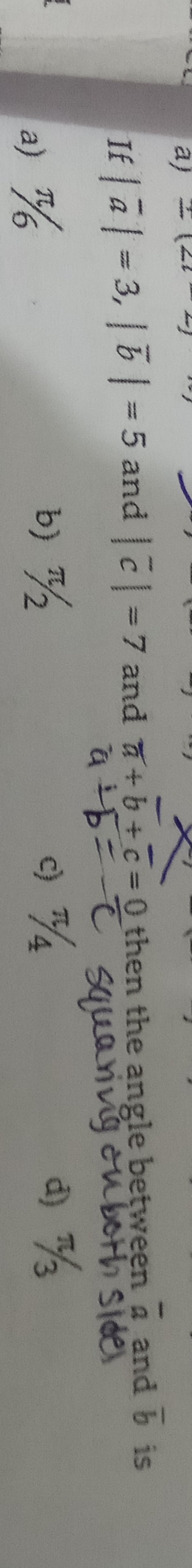
• A. $\frac{\pi}{6}$
• B. $\frac{\pi}{2}$
• C. $\frac{\pi}{4}$
• D. $\frac{\pi}{3}$

Answer 1

Answer: (D)

$\frac{\pi}{3}$

Answer 2

Given:

$$|\bar{a}| = 3, \quad |\bar{b}| = 5, \quad |\bar{c}| = 7, \quad \text{and} \quad \bar{a} + \bar{b} + \bar{c} = 0.$$

Thus,

$$\bar{a} + \bar{b} = -\bar{c}.$$

Taking magnitudes on both sides:

$$|\bar{a} + \bar{b}| = |\bar{c}| = 7.$$

Using the formula for the magnitude of the sum of two vectors:

$$|\bar{a} + \bar{b}|^2 = |\bar{a}|^2 + |\bar{b}|^2 + 2|\bar{a}||\bar{b}|\cos\theta.$$

Substitute the given values:

$$7^2 = 3^2 + 5^2 + 2(3)(5)\cos\theta,$$ $$49 = 9 + 25 + 30\cos\theta,$$ $$49 = 34 + 30\cos\theta.$$

Solve for $\cos\theta$:

$$30\cos\theta = 49 - 34 = 15,$$ $$\cos\theta = \frac{15}{30} = \frac{1}{2}.$$

Thus,

$$\theta = \arccos\left(\frac{1}{2}\right) = \frac{\pi}{3}.$$