Question
Question: If $ax^2+bx+c=0$ and $bx^2+cx+a=0$ have a common root, and a, b, c are non-zero, then $(\frac{a^3+b^...
If ax2+bx+c=0 and bx2+cx+a=0 have a common root, and a, b, c are non-zero, then (abca3+b3+c3)
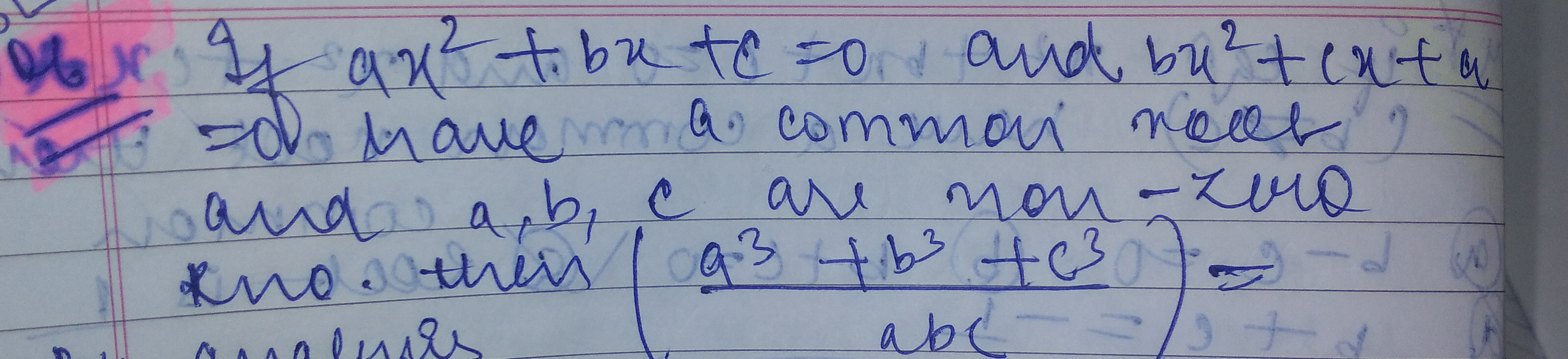
Answer
3
Explanation
Solution
The condition for two quadratic equations A1x2+B1x+C1=0 and A2x2+B2x+C2=0 to have a common root is (A1C2−A2C1)2=(A1B2−A2B1)(B1C2−B2C1). For the given equations ax2+bx+c=0 and bx2+cx+a=0, we have A1=a,B1=b,C1=c and A2=b,B2=c,C2=a. Substituting these values into the condition: (a⋅a−b⋅c)2=(a⋅c−b⋅b)(b⋅a−c⋅c) (a2−bc)2=(ac−b2)(ab−c2) Expanding both sides: a4−2a2bc+b2c2=a2bc−ac3−ab3+b2c2 a4−2a2bc=a2bc−ac3−ab3 a4+ab3+ac3=3a2bc Since a=0, divide by a: a3+b3+c3=3abc Therefore, abca3+b3+c3=abc3abc=3.
