Question
Question: If arg \[\left( {\dfrac{{z - 2i}}{{z + 2i}}} \right) = \dfrac{\pi }{6}\] then which of the following...
If arg (z+2iz−2i)=6π then which of the following options gives the correct locus of z?
A.
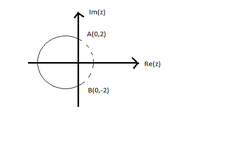
B.
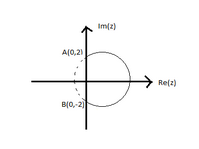
C.
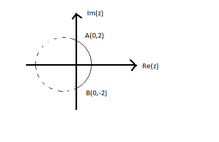
D.
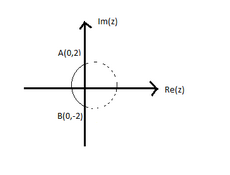
Solution
Hint : A locus is a set of all points (commonly, a line, a line segment, a curve or a surface), whose location satisfies or is determined by one or more specified conditions and for each point on the plane, arg is the function which returns the angle and here in the given options we can see that the coordinates are given with respect to real and imaginary axis with complex number z.
Complete step-by-step answer :
Let A have the coordinates (0,2) and B have the coordinates (0,−2) on the Argand plane.
Let P be the point represented by the complex number z.
z−2i represents the ray AP, while z+2i represents the ray BP.
Now, the argument of
(z+2iz−2i)=6π
Hence, when the ray BP is rotated in the anti-clockwise direction by 6π about point A, we should get ray AP.
In other words, angle BPA is always 6π .
Hence, BA must subtend a central angle of 3π on a circle.
Now, there are two possibilities, the centre can lie on the right or the left of the y axis. Since, the rotation has to be anti-clockwise, the centre has to be on the left side of the y axis.
Hence, the locus of P would be part of a circle whose centre is on the left side of the y axis.
Now, only the major arc AB will be the locus as points on the minor arc would subtend an obtuse angle.
Hence, option A is correct.
So, the correct answer is “Option A”.
Note : If you're given two points, and you're asked to find the locus of points equidistant from these two points, you'll always find the same thing: that the locus of points is actually the perpendicular bisector of the segment that joins the two points. two complex numbers are equal if and only if their real parts are equal and their imaginary parts are equal.
