Question

If area bounded by the curves $y ^ { 2 } = 4 a x$ and $y = m x$ is $\frac { a ^ { 2 } } { 3 }$, then the value of $m$ is

• A. 2
• B.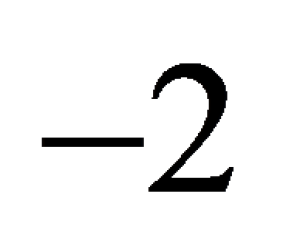
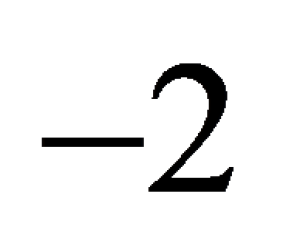
• C. $\frac { 1 } { 2 }$
• D. None of these

Answer 1

Answer: (A)

2

Answer 2

The two curves $y ^ { 2 } = 4 a x$ and $y = m x$ intersect at $\left( \frac { 4 a } { m ^ { 2 } } , \frac { 4 a } { m } \right)$ and the area enclosed by the two curves is given by $\int _ { 0 } ^ { 4 a / m ^ { 2 } } ( \sqrt { 4 a x } - m x ) d x$ .

⇒ $\frac { 8 } { 3 } \frac { a ^ { 2 } } { m ^ { 3 } } = \frac { a ^ { 2 } } { 3 } \Rightarrow m ^ { 3 } = 8 \Rightarrow m = 2$.