Solveeit Logo
Login

Question

Question: If \[\angle RPQ={{45}^{\circ }}\], find \[\angle PRQ\] A. \[{{60}^{\circ }}\] B. \[{{90}^{\circ ...

If ∠RPQ=45∘\angle RPQ={{45}^{\circ }}, find ∠PRQ\angle PRQ
A. 60∘{{60}^{\circ }}
B. 90∘{{90}^{\circ }}
C. 120∘{{120}^{\circ }}
D. 150∘{{150}^{\circ }}

Explanation

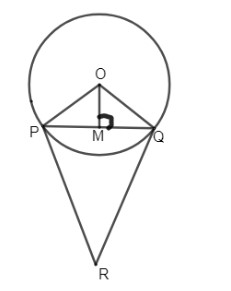
Solution

Hint: Consider, △PQR\vartriangle PQR, use the properties of the isosceles triangle and find the ∠PRQ\angle PRQ. PR and QR are tangents from a point R meeting the circle at P and Q.

“Complete step-by-step answer:”
Given a figure, with a circle whose center is O. From the figure we can say that PR and QR are tangents to the circle from a point R. Three tangents from an external point to the circle are equal.
∴PR=QR\therefore PR=QR
Now let us consider the isosceles triangle, △PRQ\vartriangle PRQ.
As it is an isosceles triangle, we know that two sides of an isosceles triangle are equal.
In △PRQ\vartriangle PRQ, we know that PR = QR.
Thus the angle RPQ is equal to angle PQR, because they are the base angles of an isosceles triangle.
We have been given, ∠RPQ=45∘\angle RPQ={{45}^{\circ }}.
∠RPQ=∠PQR=45∘\angle RPQ=\angle PQR={{45}^{\circ }}.
The angle sum property of triangle, states that the sum of interior angles of a triangle is 180∘{{180}^{\circ }}.
Hence, in the isosceles triangle PRQ, the sum of all the interior angles is 180∘{{180}^{\circ }}.
∴∠RPQ+∠PQR+∠PRQ=180∘\therefore \angle RPQ+\angle PQR+\angle PRQ={{180}^{\circ }}
We need to find the ∠PRQ\angle PRQ.
We already found out that, ∠RPQ=∠PQR=45∘\angle RPQ=\angle PQR={{45}^{\circ }}.
Thus substituting these values in the sum of triangle,

& \angle RPQ+\angle PQR+\angle PRQ={{180}^{\circ }} \\\ & {{45}^{\circ }}+{{45}^{\circ }}+\angle PRQ={{180}^{\circ }} \\\ & \angle PRQ=180-45-45=180-90 \\\ & \angle PRQ={{90}^{\circ }} \\\ \end{aligned}$$ Hence, we got $$\angle PRQ={{90}^{\circ }}$$, which makes $$\vartriangle PRQ$$ right angled at R. $$\therefore $$Option (b) is the correct answer. Note: By seeing the figure, you may try to take $$\vartriangle POQ$$ instead of $$\vartriangle PRQ$$, understand the question that we only need to find $$\angle PRQ$$. So we should take, $$\vartriangle PRQ$$. As tangents from the external point of the circle are equal, the sides of the triangle are same, thus angles are same and we can get $$\angle PRQ$$easily.