Question

If angle of repose is $30^\circ$, then coefficient of friction will be
A. $1$
B. $15$
C.$\dfrac{1}{{\sqrt 3 }}$
D.$\dfrac{{\sqrt 3 }}{2}$

Answer 1

Use the equation for the coefficient of friction for an object on a rough surface. This equation gives the relation between the coefficient of friction and the angle of repose. Substitute the value of angle of repose directly in the equation and determine the required coefficient of fiction.

Formula used:
The expression for the coefficient of friction is given by
$\mu = \tan \theta$ …… (1)
Here, $\mu$ is the coefficient of friction and $\theta$ is the angle of repose.

Complete step by step answer:
We have given that the angle of repose is $30^\circ$.
$\theta = 30^\circ$
We can determine the coefficient of friction corresponding to the given angle of repose using equation (1).
Substitute $30^\circ$ for $\theta$ in equation (1).
$\mu = \tan 30^\circ$
$\therefore \mu = \dfrac{1}{{\sqrt 3 }}$

Therefore, the coefficient of friction will be $\dfrac{1}{{\sqrt 3 }}$.Hence, the correct option is C.

Additional information:
The coefficient of friction is given by
$\mu = \dfrac{f}{N}$ …… (2)
Here, $f$ is a frictional force and $N$ is the normal force.
The formula for the coefficient of friction can be derived as follows:Draw the free-body diagram of a block of mass placed on an inclined plane.

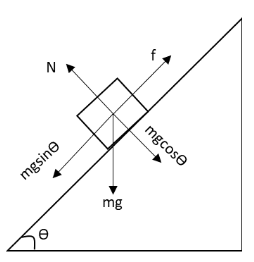
In the above figure, f is the frictional force, is the normal force on the block by the inclined surface and is the weight of the block. The components of weight of the block are also shown.Apply Newton’s second law of motion to the block in horizontal direction.
$f = mg\sin \theta$
Apply Newton’s second law of motion to the block in vertical direction.
$N = mg\cos \theta$
Substitute $mg\sin \theta$ for $f$ and $mg\cos \theta$ for $N$ in equation (2).
$\mu = \dfrac{{mg\sin \theta }}{{mg\cos \theta }}$
$\therefore \mu = tan\theta$
This is the required expression for coefficient of friction.

Note: The students should use the proper value of tan of angle of repose. One can also solve the same question by drawing the free-body diagram of a block placed on an inclined plane and deriving the formula for the coefficient of friction using the proper formula and components of the weight of the block.