Question
Question: If \(\angle B\ and\ \angle Q\) are acute angles such that \(\sin B=\sin Q\), then prove that \(\angl...
If ∠B and ∠Q are acute angles such that sinB=sinQ, then prove that ∠B=∠Q.
Solution
Hint: For the above question we will first assume two different right angled triangle say ABC and PQR and then we will use the concept that sine of any angle is equal to the ratio of perpendicular to hypotenuse of that right angled triangle and we will get the required result.
Complete step-by-step answer:
We have been given that ∠B and ∠Q are acute angles such that sinB=sinQ and we need to prove ∠B=∠Q.
Let us suppose ΔABC and ΔPQR right angled at C and R respectively.
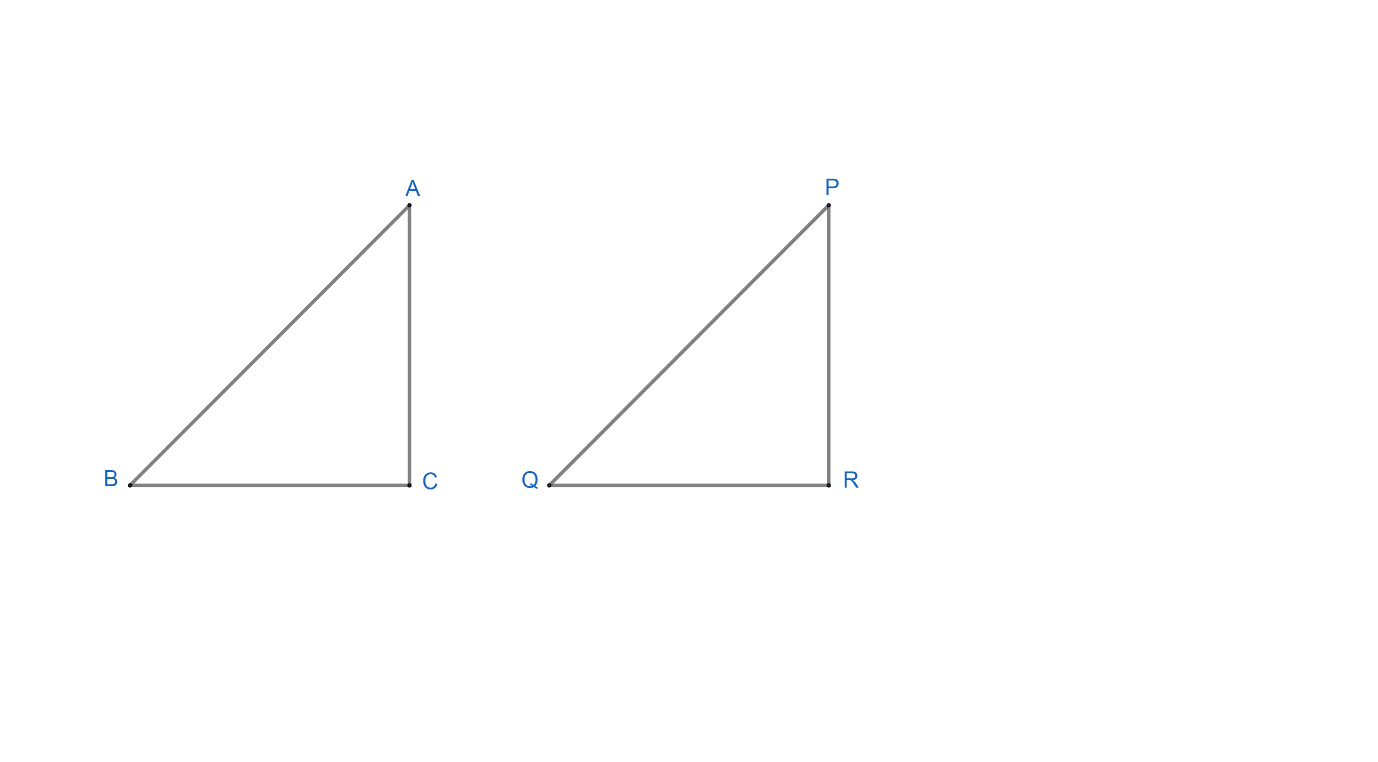
In ΔABC,
sinB=ABAC
In ΔPQR,
sinQ=PQPR
Since, sine of any angle is the ratio of perpendicular to hypotenuse.
Now, according to question we have,
sinB=sinQ⇒ABAC=PQPR⇒PRAC=PQABLet,PRAC=PQAB=K.........(1)
Now, in ΔABC, using Pythagoras theorem we have,
BC=AB2−AC2
Using (i) we get AB=K.PQ and AC=K.PR.
