Question

If $\angle A$ and $\angle B$ are acute angles such that $\tan A=\tan B$, then show that $\angle A=\angle B$.

Answer 1

Hint:To solve this question, we will require the concept of similar triangles. So, we will consider two right angled triangles, one containing $\angle A$ and the other containing $\angle B$. Then we will try to prove the triangles to be similar by using the SAS criteria to prove $\angle A=\angle B$.

Complete step-by-step answer:
In this question, we have been given that $\tan A=\tan B$, where $\angle A$ and $\angle B$ are acute angles and we are asked to prove that $\angle A=\angle B$. To prove this, we will consider two right angled triangles as shown in the figure below.

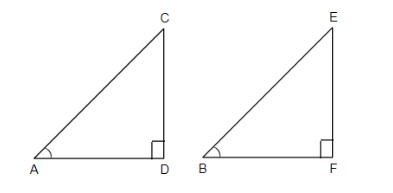
Here, in the above figure, $\Delta ADC$ and $\Delta BFE$ are two right angled triangles, right angled at $\angle D$ and $\angle F$ respectively. Now, we know that the tangent ratio of an angle is defined by the ratio of perpendicular to the base. So, we can say that,
$\tan \theta =\dfrac{Perpendicular}{Base}$
So, according to $\Delta ADC$, we can say that,
$\tan A=\dfrac{CD}{AD}\ldots \ldots \ldots \left( i \right)$
And according to $\Delta BFE$, we can say that,
$\tan B=\dfrac{EF}{BF}\ldots \ldots \ldots \left( ii \right)$
Now, we have been given in the question that, $\tan A=\tan B$. So, from equation (i) and equation (ii), we can write the equation as follows,
$\dfrac{CD}{AD}=\dfrac{EF}{BF}$
We can also write it as,
$\dfrac{CD}{EF}=\dfrac{AD}{BF}$
We also know that $\angle D=\angle F=90{}^\circ$. So, we can say by the similarity criteria SAS, $\Delta ADC\sim \Delta BFE$. Hence, all the corresponding angles of both the triangles will be congruent. Hence, we can say that, $\angle A=\angle B$.
Hence, we have proved the statement given in the question.

Note: In this question, one can think of taking tangent inverse of the given equality, which is definitely correct, but for that, we have to define the domain and range of ${{\tan }^{-1}}x$. The concept of similar triangles is a better way to solve this question.