Question
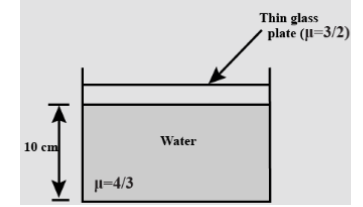
Question: If an observer sees the bottom of the vessel shown in Fig. at 8 cm, find the refractive index of the...
If an observer sees the bottom of the vessel shown in Fig. at 8 cm, find the refractive index of the medium in which the observer is present.
Solution
Calculate the apparent depth using the formula μ=apparentreal and now this becomes the real depth for the new case and 8 cm is the apparent depth and using the same formula now calculate required refractive index.
Complete step- by-step solution
When the light is travelling from medium 1 to 2 the refractive index can be written as,
1μ2=μ1μ2
If the object is placed in a different medium then due to refraction, object appears to be displaced from its real position so, when object is in denser medium and observer is in rarer medium,
μ=apparentreal
It is given that real depth is 10 cm and μ can be written as gμw=μgμw where, μg=23;μw=34
Substitute in the formula and we get apparent depth.
Using the same format the refractive index at 8 cm (μr) which is the apparent depth now
μr23=4×845 μr=1516
Hence the refractive index at 8 cm is1516 .
Note In case of more immiscible liquids as layers present then refractive index of the combination is
μc=app(d)real(d)=μ1d1+μ2d2...d1+d2...
