Question
Question: If an isosceles triangle of vertical angle \(2\theta \) is inscribed in a circle of radius \(a\). Th...
If an isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a. Then, area of the triangle is maximum, when θ is equal to
A. 6π
B. 4π
C. 3π
D. 2π
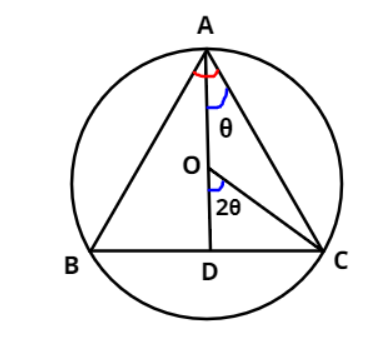
Solution
Hint- We will be using an inscribed angle theorem to evaluate the base and height of the triangle which will help in finding the area of the triangle.
In the figure, △ABC is an isosceles triangle with AB=AC.
Also it is given that ∠A=∠BAC=2θ (shown in the figure as marked by red arc)
The centre of the circle is O and radius OC=OA=a
Now, let us draw an angle bisector AD from the vertex A of the isosceles triangle which divides ∠A=∠BAC=2θ into two equal angles i.e., ∠BAD=∠CAD=22θ=θ.
According to the inscribed angle theorem, we can say that ∠COD will be twice ∠CAD.
i.e., ∠COD=2(∠CAD)=2θ
In right angled triangle ODC,
cos(2θ)=HypotenuseBase=OCOD=aOD⇒OD=a[cos(2θ)]
Also, sin(2θ)=HypotenusePerpendicular=OCDC=aDC⇒DC=a[sin(2θ)]
Now, BC=2(DC)=2a[sin(2θ)] and AD=OD+OA=a[cos(2θ)]+a=a[cos(2θ)+1]
As we know that Area of a triangle=21×(Base)×(Height)
Area of △ABC, A=21×(BC)×(AD)=21×(2a[sin(2θ)])×(a[cos(2θ)+1])=a2[sin(2θ)cos(2θ)+sin(2θ)]
Also we know that sin(2α)=2(sinα)(cosα)⇒(sinα)(cosα)=2sin(2α)
⇒A=a2[sin(2θ)cos(2θ)+sin(2θ)]⇒A=a2[2sin(4θ)+sin(2θ)]
Now differentiating above equation with respect to θ both sides, we get
Now, for area of the triangle to be maximum put dθdA=0
⇒0=2a2[cos(4θ)+cos(2θ)]⇒cos(4θ)+cos(2θ)=0⇒θ=2π,6π
Now, differentiating equation (1) again with respect to θ, we have
For θ=2π, dθ2d2A=−4a2[2sin(4×2π)+sin(2×2π)]=−4a2[2sin(2π)+sin(π)]=−4a2[2×0+0]=0
For θ=6π, dθ2d2A=−4a2[2sin(4×6π)+sin(2×6π)]=−4a2[2sin(32π)+sin(3π)]=−4a2[2×23+23]=−63a2
As, we know that area of the triangle will be maximum where dθ2d2A<0 i.e., will be negative .
So, at θ=6π, the area of the given triangle is maximum.
Therefore, option A is correct.
Note- The inscribed angle theorem states that an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle. Also, here For θ=2π, the double derivative of the area of the triangle comes out to be zero which means it is an inflection point.
