Question

If an equilateral triangle is inscribed in a circle and the triangle’s area is $4\sqrt 3$. What is the area of the circle?

Answer 1

Hint : Here, in the given question, we are given that the area of an equilateral triangle which is inscribed in a circle is $4\sqrt 3$, and we need to find the area of the circle. So, to find the area of a circle, we first need to find the radius of the circle. Let us first draw a figure using the information provided in the question. We will connect the center of the circle to the vertices of the triangle, this will be our radius. As we are given that the triangle is equilateral, so by using triangle $PQR$, we will find the value of side and after that, by using triangle $QSO$, we will find the value of radius and substitute in the general formula of area of triangle to get our required answer.
Formula used :
Area of triangle = $\dfrac{1}{2} \times base \times height$
Area of circle = $\pi {r^2}$

Complete step-by-step answer :

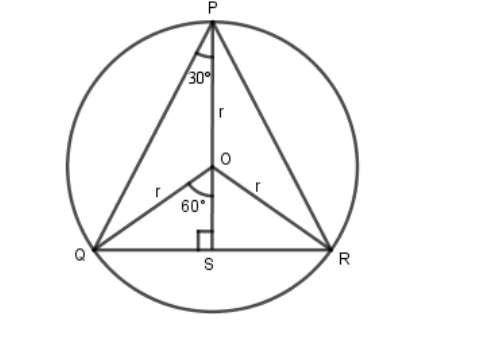
Considering the triangle $PQS$:
Since the triangle $PQR$ is equilateral, its internal angles are equal to $60^\circ$ and a circle’s radius with an endpoint in the triangle vertex $P$ bisects the internal angle $\angle QPR$ in two angles, $\angle QPS$ and $\angle SPR$, of $30^\circ$ each.
$\Rightarrow \tan \angle QPS = \tan 30^\circ$
As we know $\tan = \dfrac{P}{B}$. Therefore, we get
$\Rightarrow \tan 30^\circ = \dfrac{{\dfrac{{side}}{2}}}{{height}}$
On cross multiplication, we get
$\Rightarrow height = \dfrac{{\dfrac{{side}}{2}}}{{\tan 30^\circ }}$
As we know $\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$. Therefore, we get
$\Rightarrow height = \dfrac{{\dfrac{{side}}{2}}}{{\dfrac{1}{{\sqrt 3 }}}} = \dfrac{{side}}{2} \times \dfrac{{\sqrt 3 }}{1}$
$\Rightarrow height = \dfrac{{\sqrt 3 }}{2} \times side$
As we know the area of the triangle is $\dfrac{1}{2} \times base \times height$.
Area of a given equilateral triangle is $4\sqrt 3$.
$\Rightarrow 4\sqrt 3 = \dfrac{1}{2} \times side \times \dfrac{{\sqrt 3 }}{2} \times side$
On simplification, we get
$\Rightarrow 4\sqrt 3 = \dfrac{{\sqrt 3 }}{4} \times sid{e^2}$
On canceling out common terms, we get
$\Rightarrow 4 = \dfrac{{sid{e^2}}}{4}$
On cross multiplication, we get
$\Rightarrow sid{e^2} = 16$
$\Rightarrow side = 4unit$
Considering the triangle $QSO$:
All the three triangles resulting from the division of the triangle $PQR$ by the circle’s radius with endpoints in $P$, $Q$ and $R$ (triangles $PQO$, $QRO$ and $PRO$) are congruent. So since their obtuse angles are equal and sum $360^\circ$ ($\angle POQ + \angle QOR + \angle POR = 360^\circ$), each one of them must be equal to $\dfrac{{360^\circ }}{3} = 120^\circ$. Since the triangles $QSO$ and $RSO$ are congruent, $\angle QOS = \angle ROS$, and since they sum $120^\circ$ ($= \angle QOR$), each of them is equal to $60^\circ$).
$\Rightarrow \sin \angle QOS = \sin 60^\circ$
As we know $\sin = \dfrac{P}{H}$. Therefore, we get
$\Rightarrow \sin 60^\circ = \dfrac{{\dfrac{{side}}{2}}}{r}$
$\Rightarrow r = \dfrac{{\dfrac{{side}}{2}}}{{\sin 60^\circ }}$
As we know $\sin 60^\circ = \dfrac{{\sqrt 3 }}{2}$. Therefore, we get
$\Rightarrow r = \dfrac{{\dfrac{{side}}{2}}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{side}}{2} \times \dfrac{2}{{\sqrt 3 }}unit$
$\Rightarrow r = \dfrac{4}{2} \times \dfrac{2}{{\sqrt 3 }}unit$
On canceling out common terms, we get
$\Rightarrow r = \dfrac{4}{{\sqrt 3 }}unit$
Area of circle = $\pi {r^2}$
On substituting value of radius, we get
Area of circle = $\pi {\left( {\dfrac{4}{{\sqrt 3 }}} \right)^2}sq.unit$
On squaring, we get
Area of circle = $\pi \times \dfrac{{16}}{3}sq.unit$
Area of circle = $\dfrac{{16\pi }}{3}sq.unit$
So, the correct answer is “$\dfrac{{16\pi }}{3}sq.unit$”.

Note : To solve these type of questions we should know all the required values of standard angles say, $0^\circ ,30^\circ ,60^\circ ,90^\circ ,180^\circ ,270^\circ ,360^\circ$ respectively for each trigonometric term such as $\sin ,\cos ,\tan ,\cos ec,\sec ,\cot$. Also, to solve this type of question, one must remember all the formulas of area, perimeter, etc. of different figures. We wrote the side only in positive value because the side can’t be negative as it is the length. We should take care of the calculations so as to be sure of our final answer. Remember to write units.