Question

If an equilateral triangle, having centroid at the origin, has a side along the line, $x+y=2$, then the area (in sq. units) of this triangle is:
A. $6$
B. $6\sqrt{3}$
C. $\dfrac{9}{2}\sqrt{3}$
D. $3\sqrt{6}$

Answer 1

In this question we have to find out the area of the equilateral triangle, so, first of all we have to find out the side of the triangle. Once we find the length of triangle we can find the area of equilateral triangle by using the formula $A=\dfrac{\sqrt{3}}{4}{{a}^{2}}$ where $a$is the length of side of triangle .
Its origin is the centroid of the equilateral triangle so here we use the property that centroid divides the median in $2:1$ ratio. Also use perpendicular distance formula to find the perpendicular distance between centroid and the side of triangle using the formula, if $ax+by+c=0$ be any straight line and $\left( \alpha ,\beta \right)$be any point then perpendicular distance is given by
$d=\dfrac{a\alpha +b\beta +c}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$

Complete step-by-step answer:
First we draw the figure as below

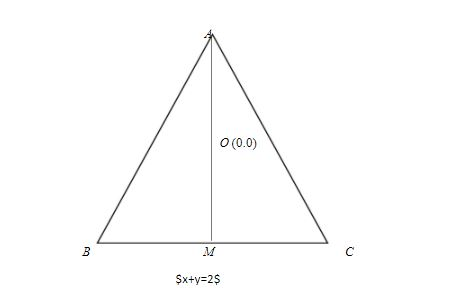
Let AB, BC, AC be the sides of the equilateral triangle. Let $AB=BC=CA=a$. Let O is the origin of the triangle and side BC is along the straight line $x+y=2$, OM is the perpendicular distance from O to BC, so we can find OM by using the formula
$d=\left| \dfrac{a\alpha +b\beta +c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$
As we have equation of straight line $x+y-2=0$ and $\left( \alpha ,\beta \right)$is $(0,0)$
So, we have $a=1,\text{ }b=1,\text{ }c=-1$
Hence, we have
$\begin{aligned} & d=\left| \dfrac{1.(0)+1(0)-2}{\sqrt{{{1}^{2}}+{{1}^{2}}}} \right| \\\ & d=\left| \dfrac{-2}{\sqrt{2}} \right| \\\ & d=\sqrt {2} \\\ \end{aligned}$
So here we find OM
As we know that centroid divides the median AM in $2:1$ratio
Hence, we can write
$\dfrac{AO}{OM}=\dfrac{2}{1}$
Adding both side 1 we have

& \dfrac{AO}{OM}+1=\dfrac{2}{1}+1 \\\ & \dfrac{AO+OM}{OM}=3 \\\ & \dfrac{AM}{OM}=3 \\\ & AM=3OM \\\ & AM=3\sqrt{2} \\\ \end{aligned}$$ As we Median AM bisect the side of the equilateral triangle, also median AM is perpendicular to the side of triangle BC. So, we can write, $$BM=MC=\dfrac{a}{2}$$ And in right angle triangle AMC, we can use Pythagora's theorem in order to find the side AC. Hence, we can write $\begin{aligned} & A{{C}^{2}}=A{{M}^{2}}+M{{C}^{2}} \\\ & {{a}^{2}}={{\left( 3\sqrt{2} \right)}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}} \\\ & {{a}^{2}}-\dfrac{{{a}^{2}}}{4}=18 \\\ & \dfrac{4{{a}^{2}}-{{a}^{2}}}{4}=9 \\\ & 3{{a}^{2}}=(18)(4) \\\ & {{a}^{2}}=24-------(a) \\\ \end{aligned}$ As we know that area of equilateral triangle is given by $A=\dfrac{\sqrt{3}}{4}{{a}^{2}}$ So, putting the value of ${{a}^{2}}=24$ from equation $(a)$ we can find the area of triangle $$\begin{aligned} & A=\dfrac{\sqrt{3}}{4}(24) \\\ & A=6\sqrt{3} \\\ \end{aligned}$$ Hence, we find the area of the equilateral triangle is $6\sqrt{3}$square unit. Hence, option B is correct. **Note:** Line joining the vertices and centroid of triangle bisect the angle so $\angle OCM=30{}^\circ $. we can find OM by using trigonometry also. Centroid is the point of intersection of median. Median is the line joining of midpoint of side and opposite vertices. So, centroid of a triangle always lies inside the triangle. In an equilateral triangle centroid, incentre, orthocentre all are same points.