Question

If $\alpha_1, \beta_1$ are the roots of the equation $ax^2 + bx + c = 0$ and $\alpha_2, \beta_2$ are the roots of the equation $px^2 + qx + r = 0$ if $a, b$ and $c$ are in GP as well as $\alpha_1, \beta_1, \alpha_2, \beta_2$ are in GP, then $p, q$ and $r$ are in

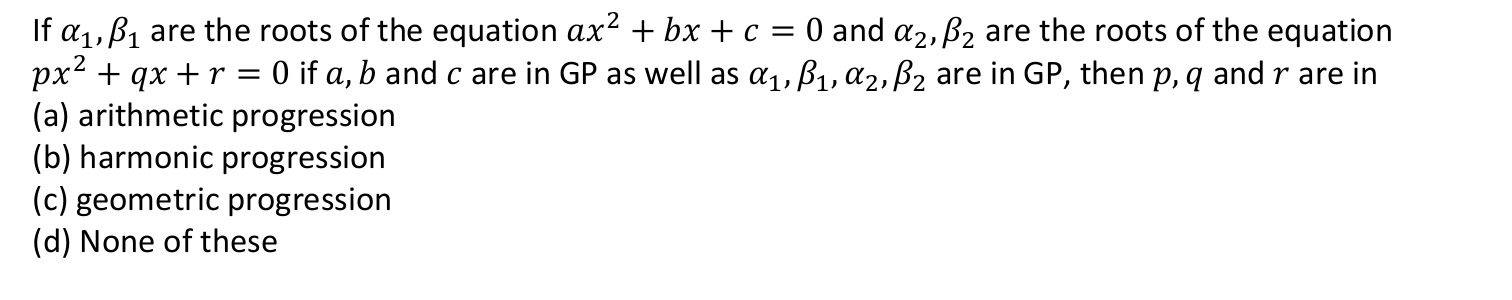
• A. arithmetic progression
• B. harmonic progression
• C. geometric progression
• D. None of these

Answer 1

Answer: (C)

geometric progression

Answer 2

Let the first quadratic equation be $ax^2 + bx + c = 0$ with roots $\alpha_1, \beta_1$.

It is given that $a, b, c$ are in GP. Let the common ratio be $k$. Then $b = ak$ and $c = ak^2$. Since $a, b, c$ are coefficients of a quadratic equation, $a \neq 0$. The equation becomes $ax^2 + akx + ak^2 = 0$. Dividing by $a$, we get $x^2 + kx + k^2 = 0$. The roots $\alpha_1, \beta_1$ satisfy: $\alpha_1 + \beta_1 = -k$ $\alpha_1 \beta_1 = k^2$

The roots of $x^2 + kx + k^2 = 0$ are given by the quadratic formula: $x = \frac{-k \pm \sqrt{k^2 - 4k^2}}{2} = \frac{-k \pm \sqrt{-3k^2}}{2} = \frac{-k \pm ik\sqrt{3}}{2}$. These roots are $k \left(\frac{-1 + i\sqrt{3}}{2}\right)$ and $k \left(\frac{-1 - i\sqrt{3}}{2}\right)$. Let $\omega = e^{i2\pi/3} = \frac{-1 + i\sqrt{3}}{2}$ and $\omega^2 = e^{i4\pi/3} = \frac{-1 - i\sqrt{3}}{2}$. Note that $\omega^3 = 1$ and $1+\omega+\omega^2 = 0$. The roots $\alpha_1, \beta_1$ are $\{k\omega, k\omega^2\}$.

It is given that $\alpha_1, \beta_1, \alpha_2, \beta_2$ are in GP. Let the common ratio of this GP be $m$. The terms are $\alpha_1, \alpha_1 m, \alpha_1 m^2, \alpha_1 m^3$. So, $\beta_1 = \alpha_1 m$, $\alpha_2 = \alpha_1 m^2$, $\beta_2 = \alpha_1 m^3$.

From $\beta_1 = \alpha_1 m$, the common ratio $m = \beta_1 / \alpha_1$. If $\alpha_1 = k\omega$ and $\beta_1 = k\omega^2$, then $m = \frac{k\omega^2}{k\omega} = \omega$. If $\alpha_1 = k\omega^2$ and $\beta_1 = k\omega$, then $m = \frac{k\omega}{k\omega^2} = \frac{1}{\omega} = \omega^2$. So the common ratio $m$ of the GP of roots is either $\omega$ or $\omega^2$.

Case 1: $m = \omega$. Let $\alpha_1 = k\omega$. Then $\beta_1 = \alpha_1 m = k\omega \cdot \omega = k\omega^2$. This is consistent. The terms of the GP are: $\alpha_1 = k\omega$ $\beta_1 = k\omega^2$ $\alpha_2 = \alpha_1 m^2 = k\omega \cdot \omega^2 = k\omega^3 = k$ $\beta_2 = \alpha_1 m^3 = k\omega \cdot \omega^3 = k\omega^4 = k\omega$ The roots of the second equation $px^2 + qx + r = 0$ are $\alpha_2 = k$ and $\beta_2 = k\omega$. Sum of roots: $\alpha_2 + \beta_2 = k + k\omega = k(1+\omega) = k(-\omega^2)$. Product of roots: $\alpha_2 \beta_2 = k \cdot k\omega = k^2\omega$.

From the equation $px^2 + qx + r = 0$: $\alpha_2 + \beta_2 = -q/p$ $\alpha_2 \beta_2 = r/p$ So, $-q/p = -k\omega^2 \implies q/p = k\omega^2 \implies q = pk\omega^2$. And $r/p = k^2\omega \implies r = pk^2\omega$.

We check if $p, q, r$ are in GP, i.e., $q^2 = pr$. $q^2 = (pk\omega^2)^2 = p^2k^2\omega^4 = p^2k^2\omega$ (since $\omega^4 = \omega^3 \cdot \omega = \omega$). $pr = p(pk^2\omega) = p^2k^2\omega$. Since $q^2 = pr$, $p, q, r$ are in GP.

Case 2: $m = \omega^2$. Let $\alpha_1 = k\omega^2$. Then $\beta_1 = \alpha_1 m = k\omega^2 \cdot \omega^2 = k\omega^4 = k\omega$. This is consistent. The terms of the GP are: $\alpha_1 = k\omega^2$ $\beta_1 = k\omega$ $\alpha_2 = \alpha_1 m^2 = k\omega^2 \cdot (\omega^2)^2 = k\omega^6 = k(\omega^3)^2 = k$ $\beta_2 = \alpha_1 m^3 = k\omega^2 \cdot (\omega^2)^3 = k\omega^8 = k(\omega^3)^2 \cdot \omega^2 = k\omega^2$ The roots of the second equation $px^2 + qx + r = 0$ are $\alpha_2 = k$ and $\beta_2 = k\omega^2$. Sum of roots: $\alpha_2 + \beta_2 = k + k\omega^2 = k(1+\omega^2) = k(-\omega)$. Product of roots: $\alpha_2 \beta_2 = k \cdot k\omega^2 = k^2\omega^2$.

From the equation $px^2 + qx + r = 0$: $-q/p = -k\omega \implies q/p = k\omega \implies q = pk\omega$. $r/p = k^2\omega^2 \implies r = pk^2\omega^2$.

We check if $p, q, r$ are in GP, i.e., $q^2 = pr$. $q^2 = (pk\omega)^2 = p^2k^2\omega^2$. $pr = p(pk^2\omega^2) = p^2k^2\omega^2$. Since $q^2 = pr$, $p, q, r$ are in GP.

In both possible cases for the common ratio of the GP of roots, we find that $p, q, r$ are in GP.