Question

If $\alpha_1, \alpha_1, \alpha_2, \alpha_3,........\alpha_n$ are the roots of equation $x^{n+1}-5x^2+6x-3=0$ and $(\alpha_1 - \alpha_2)(\alpha_1 - \alpha_3)(\alpha_1 - \alpha_4)....(\alpha_1 - \alpha_n)=k$, then $n(n+1)\alpha_1^{n-1}-2k$ equals

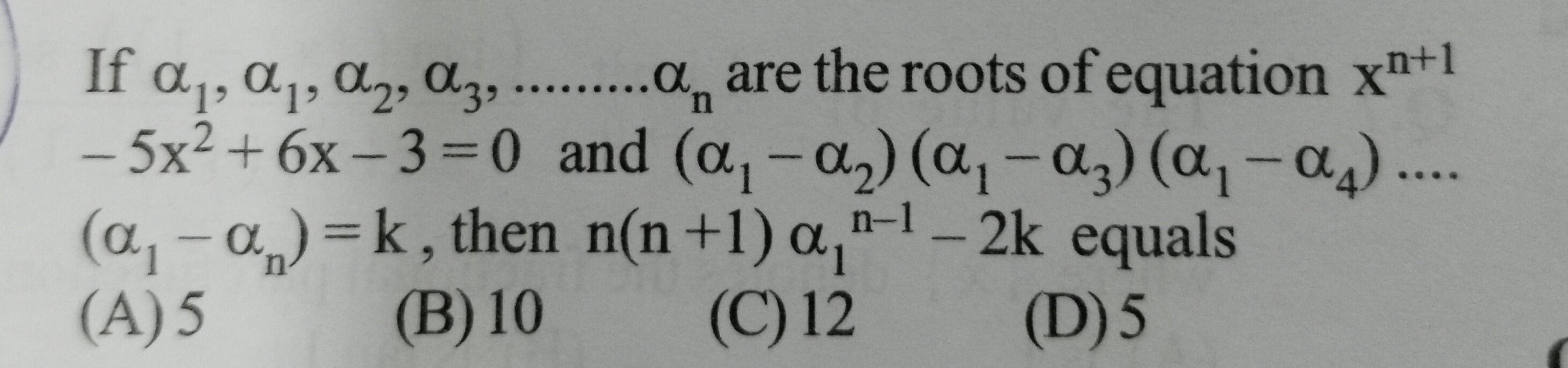
• A. 5
• B. 10
• C. 12
• D. 5

Answer 1

Answer: (B)

10

Answer 2

Let the given polynomial be $P(x) = x^{n+1}-5x^2+6x-3$. The roots of the equation $P(x)=0$ are given as $\alpha_1, \alpha_1, \alpha_2, \alpha_3, \ldots, \alpha_n$. This means $\alpha_1$ is a root with multiplicity at least 2, and $\alpha_2, \ldots, \alpha_n$ are the other $n-1$ roots. The total number of roots is $2 + (n-1) = n+1$, which matches the degree of the polynomial $P(x)$.

Since $\alpha_1$ is a root of $P(x)$ with multiplicity at least 2, it must satisfy $P(\alpha_1)=0$ and $P'(\alpha_1)=0$. $P(x) = x^{n+1}-5x^2+6x-3$ $P'(x) = \frac{d}{dx}(x^{n+1}-5x^2+6x-3) = (n+1)x^n - 10x + 6$.

Since $P'(\alpha_1)=0$, we have $(n+1)\alpha_1^n - 10\alpha_1 + 6 = 0$.

Let the roots of $P(x)$ be $r_1, r_2, \ldots, r_{n+1}$. In this case, $r_1=\alpha_1, r_2=\alpha_1, r_3=\alpha_2, \ldots, r_{n+1}=\alpha_n$. The polynomial can be written as $P(x) = (x-r_1)(x-r_2)\cdots(x-r_{n+1})$. $P(x) = (x-\alpha_1)(x-\alpha_1)(x-\alpha_2)\cdots(x-\alpha_n)$. Let $Q(x) = (x-\alpha_2)(x-\alpha_3)\cdots(x-\alpha_n)$. Then $P(x) = (x-\alpha_1)^2 Q(x)$.

We are given $k = (\alpha_1 - \alpha_2)(\alpha_1 - \alpha_3)(\alpha_1 - \alpha_4)....(\alpha_1 - \alpha_n)$. This expression is equal to $Q(\alpha_1)$. So, $k = Q(\alpha_1)$.

Now, let's consider the derivative of $P(x)$: $P'(x) = \frac{d}{dx}[(x-\alpha_1)^2 Q(x)] = 2(x-\alpha_1)Q(x) + (x-\alpha_1)^2 Q'(x)$. $P'(x) = (x-\alpha_1)[2Q(x) + (x-\alpha_1)Q'(x)]$.

Since $\alpha_1$ is a root of $P(x)$ with multiplicity at least 2, $P'(\alpha_1)=0$, which is confirmed by the expression for $P'(x)$: $P'(\alpha_1) = (\alpha_1-\alpha_1)[2Q(\alpha_1) + (\alpha_1-\alpha_1)Q'(\alpha_1)] = 0$.

Now, let's consider the second derivative of $P(x)$: $P''(x) = \frac{d}{dx}[(x-\alpha_1)[2Q(x) + (x-\alpha_1)Q'(x)]]$. Let $R(x) = 2Q(x) + (x-\alpha_1)Q'(x)$. Then $P'(x) = (x-\alpha_1)R(x)$. $P''(x) = 1 \cdot R(x) + (x-\alpha_1)R'(x)$. $P''(x) = [2Q(x) + (x-\alpha_1)Q'(x)] + (x-\alpha_1)[2Q'(x) + Q'(x) + (x-\alpha_1)Q''(x)]$. $P''(x) = 2Q(x) + (x-\alpha_1)Q'(x) + (x-\alpha_1)[3Q'(x) + (x-\alpha_1)Q''(x)]$. $P''(x) = 2Q(x) + 4(x-\alpha_1)Q'(x) + (x-\alpha_1)^2Q''(x)$.

Now, evaluate $P''(x)$ at $x=\alpha_1$: $P''(\alpha_1) = 2Q(\alpha_1) + 4(\alpha_1-\alpha_1)Q'(\alpha_1) + (\alpha_1-\alpha_1)^2Q''(\alpha_1)$. $P''(\alpha_1) = 2Q(\alpha_1) + 0 + 0 = 2Q(\alpha_1)$. Since $k = Q(\alpha_1)$, we have $P''(\alpha_1) = 2k$.

Now, let's compute the second derivative of $P(x)$ from its given form: $P'(x) = (n+1)x^n - 10x + 6$ $P''(x) = \frac{d}{dx}((n+1)x^n - 10x + 6) = (n+1)nx^{n-1} - 10$.

Evaluate $P''(x)$ at $x=\alpha_1$: $P''(\alpha_1) = (n+1)n\alpha_1^{n-1} - 10$.

Equating the two expressions for $P''(\alpha_1)$: $(n+1)n\alpha_1^{n-1} - 10 = 2k$. We are asked to find the value of $n(n+1)\alpha_1^{n-1}-2k$. Rearranging the equation: $n(n+1)\alpha_1^{n-1} - 2k = 10$.

The value of $n(n+1)\alpha_1^{n-1}-2k$ is 10.