Solveeit Logo
Login

Question

Question: If \(\alpha ={{\cos }^{-1}}\left( \dfrac{3}{5} \right),\beta ={{\tan }^{-1}}\left( \dfrac{1}{3} \rig...

If α=cos⁡−1(35),β=tan⁡−1(13)\alpha ={{\cos }^{-1}}\left( \dfrac{3}{5} \right),\beta ={{\tan }^{-1}}\left( \dfrac{1}{3} \right) where 0<α,β<π2,0<\alpha ,\beta <\dfrac{\pi }{2},then α−β\alpha -\beta is equal to:
A. sin⁡−1(9510){{\sin }^{-1}}\left( \dfrac{9}{5\sqrt{10}} \right)
B. tan⁡−1(914){{\tan }^{-1}}\left( \dfrac{9}{14} \right)
C. cos⁡−1(9510){{\cos }^{-1}}\left( \dfrac{9}{5\sqrt{10}} \right)
D. tan⁡−1(9510){{\tan }^{-1}}\left( \dfrac{9}{5\sqrt{10}} \right)

Explanation

Solution

Hint: Using the basic definition of the trigonometric ratio first find the values of the sides of the triangle. Then apply Pythagoras theorem to find the other side of the triangle. Next find the values of sin, cos, tan\text{sin, cos, tan} of α,β\alpha ,\beta respectively and then simplify to get the result.

Complete step-by-step answer:
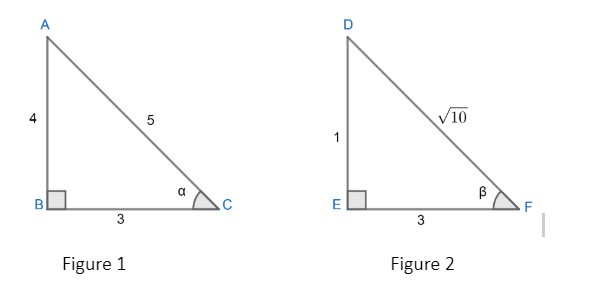
In the question we are given α=cos⁡−1(35) and β=tan⁡−1(13)\alpha ={{\cos }^{-1}}\left( \dfrac{3}{5} \right)\text{ and }\beta ={{\tan }^{-1}}\left( \dfrac{1}{3} \right)
Now, let’s consider a right angled triangle with an included angle ′α′'\alpha ' and another right angled triangle with an included angle ′β′'\beta ' which is shown in figure 1 and figure 2 respectively.

F
We are given α=cos⁡−1(35)\alpha ={{\cos }^{-1}}\left( \dfrac{3}{5} \right)
⇒cos⁡α=35\Rightarrow \cos \alpha =\dfrac{3}{5}
But we know, cos⁡θ=adjacent sidehypotenuse\cos \theta =\dfrac{\text{adjacent side}}{hypotenuse} , so in ΔABC,\Delta ABC,
cos⁡α=BCAC=35\cos \alpha =\dfrac{BC}{AC}=\dfrac{3}{5}
So, by Pythagoras theorem, we have
AB=(AC)2−(BC)2 AB=52−32=4 \begin{aligned} & AB=\sqrt{{{\left( AC \right)}^{2}}-{{\left( BC \right)}^{2}}} \\\ & AB=\sqrt{{{5}^{2}}-{{3}^{2}}}=4 \\\ \end{aligned}
Now we know, sinθ=opposite sidehypotenusesin\theta =\dfrac{\text{opposite side}}{hypotenuse}, so we get
sin⁡α=ABAC\sin \alpha =\dfrac{AB}{AC}
Substituting the corresponding values, we get
sin⁡α=45\sin \alpha =\dfrac{4}{5}
Now we know, tan⁡θ=sin⁡θcos⁡θ\tan \theta =\dfrac{\sin \theta }{\cos \theta } , so we can write
tanα=sin⁡αcos⁡αtan\alpha =\dfrac{\sin \alpha }{\cos \alpha }
Substituting the corresponding values, we get
tanα=4535=43tan\alpha =\dfrac{\dfrac{4}{5}}{\dfrac{3}{5}}=\dfrac{4}{3}
Now we got all the sine, cosine and tan of ′α′'\alpha '.
Now consider figure 2;
We are given,
β=tan⁡−1(13)\beta ={{\tan }^{-1}}\left( \dfrac{1}{3} \right)
⇒tan⁡β=13\Rightarrow \tan \beta =\dfrac{1}{3}
Now we know, tanθ=opposite sideadjacent sidetan\theta =\dfrac{\text{opposite side}}{\text{adjacent side}}.
In ΔDEF,\Delta DEF,, we can write
tan⁡β=DEEF=13\tan \beta =\dfrac{DE}{EF}=\dfrac{1}{3}
So, by Pythagoras theorem, we have

& {{\left( DF \right)}^{2}}={{\left( DE \right)}^{2}}+{{\left( EF \right)}^{2}} \\\ & DF=\sqrt{{{1}^{2}}+{{3}^{2}}}=\sqrt{10} \\\ \end{aligned}$$ Using the value of sides of the triangle, we will find the corresponding sine, cosine values. $\sin \beta =\dfrac{DE}{DF}=\dfrac{1}{\sqrt{10}}$ Now we know, $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ , so we can write $tan\beta =\dfrac{\sin \beta }{\cos \beta }$ Substituting the corresponding values, we get $\begin{aligned} & \Rightarrow \dfrac{1}{3}=\dfrac{\dfrac{1}{\sqrt{10}}}{\cos \beta } \\\ & \Rightarrow \cos \beta =\dfrac{3}{\sqrt{10}} \\\ \end{aligned}$ Now we got all the sine, cosine and tan of $'\beta '$. Now, we will use the identity, $\sin \left( \alpha -\beta \right)=\sin \alpha \cos \beta -\cos \alpha \sin \beta $ We know the values of $\sin \alpha ,\cos \alpha ,\sin \beta \text{ and }\cos \beta $. So, by substituting we get; $$\begin{aligned} & \sin \left( \alpha -\beta \right)=\dfrac{4}{5}\times \dfrac{3}{\sqrt{10}}-\dfrac{3}{5}\times \dfrac{1}{\sqrt{10}} \\\ & \sin \left( \alpha -\beta \right)=\dfrac{12-3}{5\sqrt{10}}=\dfrac{9}{5\sqrt{10}} \\\ \end{aligned}$$ Now, we see that; $\sin \left( \alpha -\beta \right)=\dfrac{9}{5\sqrt{10}}$ Then $\left( \alpha -\beta \right)={{\sin }^{-1}}\left( \dfrac{9}{5\sqrt{10}} \right)$ Now, we will use the identity, $\cos \left( \alpha -\beta \right)=\cos \alpha \cos \beta +\sin \alpha \sin \beta $ We know the values of $\sin \alpha ,\cos \alpha ,\sin \beta \text{ and }\cos \beta $. So, by substituting we get; $\begin{aligned} & \cos \left( \alpha -\beta \right)=\dfrac{3}{5}\times \dfrac{3}{\sqrt{10}}+\dfrac{4}{5}\times \dfrac{1}{\sqrt{10}} \\\ & =\dfrac{9}{5\sqrt{10}}+\dfrac{4}{5\sqrt{10}}=\dfrac{13}{5\sqrt{10}} \\\ \end{aligned}$ Now, we see that; $\cos \left( \alpha -\beta \right)=\dfrac{13}{5\sqrt{10}}$ Then $\left( \alpha -\beta \right)={{\cos }^{-1}}\left( \dfrac{13}{5\sqrt{10}} \right)$ Now, we will use the identity, $\tan \left( \alpha -\beta \right)=\dfrac{\sin \left( \alpha -\beta \right)}{\cos \left( \alpha -\beta \right)}$ As, we got that $\sin \left( \alpha -\beta \right)=\dfrac{9}{5\sqrt{10}}\text{ and cos}\left( \alpha -\beta \right)=\dfrac{13}{5\sqrt{10}}$ So, $\tan \left( \alpha -\beta \right)=\dfrac{9}{13}$ Then$\left( \alpha -\beta \right)={{\tan }^{-1}}\left( \dfrac{9}{13} \right)$ So, the correct answer is option A. Note: The identities of all the trigonometric ratios must be known by heart by the students to work on these kinds of problems at a quick pace. Also, the calculation part must be done with care to avoid silly mistakes. Student generally calculate the value of $\left( \alpha -\beta \right)={{\sin }^{-1}}\left( \dfrac{9}{5\sqrt{10}} \right)$, then they stop thinking we got the answer. But they should find other values too for comparing.