Question
Question: If $\alpha, \beta, \gamma, \sigma$ are the roots of the equation $x^4 + 4x^3 - 6x^2 + 7x - 9 = 0$ t...
If α,β,γ,σ are the roots of the equation
x4+4x3−6x2+7x−9=0 then the value of
(1+α2)(1+β2)(1+γ2)(1+σ2) is
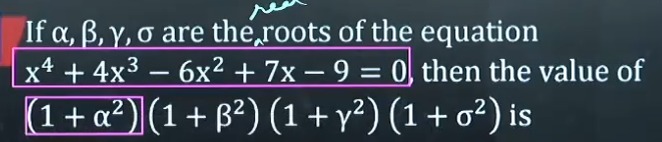
13
Solution
The given polynomial equation is P(x)=x4+4x3−6x2+7x−9=0. Let its roots be α,β,γ,σ.
Since the leading coefficient of the polynomial is 1, we can express P(x) in terms of its roots as: P(x)=(x−α)(x−β)(x−γ)(x−σ).
We need to find the value of the product (1+α2)(1+β2)(1+γ2)(1+σ2). We can rewrite each term (1+r2) as (r−i)(r+i), where i=−1. So, the expression becomes:
(1+α2)(1+β2)(1+γ2)(1+σ2)=(α−i)(α+i)(β−i)(β+i)(γ−i)(γ+i)(σ−i)(σ+i)
Rearrange the terms by grouping those with (r−i) and (r+i):
=[(α−i)(β−i)(γ−i)(σ−i)]×[(α+i)(β+i)(γ+i)(σ+i)]
Now, let's relate these products to the polynomial P(x):
- Consider P(i):
P(i)=(i−α)(i−β)(i−γ)(i−σ).
We can factor out (−1) from each term in the first bracket of our expression:
(α−i)(β−i)(γ−i)(σ−i)=(−1)4(i−α)(i−β)(i−γ)(i−σ)=P(i).
- Consider P(−i):
P(−i)=(−i−α)(−i−β)(−i−γ)(−i−σ).
We can factor out (−1) from each term in the second bracket of our expression:
(α+i)(β+i)(γ+i)(σ+i)=(−1)4(−α−i)(−β−i)(−γ−i)(−σ−i)=P(−i).
Therefore, the value we need to find is P(i)×P(−i).
First, calculate P(i):
P(i)=i4+4i3−6i2+7i−9
Using the properties of i: i2=−1, i3=−i, i4=1.
P(i)=(1)+4(−i)−6(−1)+7i−9
P(i)=1−4i+6+7i−9
P(i)=(1+6−9)+(−4+7)i
P(i)=−2+3i.
Next, calculate P(−i):
P(−i)=(−i)4+4(−i)3−6(−i)2+7(−i)−9
P(−i)=(1)+4(i)−6(−1)−7i−9
P(−i)=1+4i+6−7i−9
P(−i)=(1+6−9)+(4−7)i
P(−i)=−2−3i.
Finally, multiply P(i) and P(−i):
(1+α2)(1+β2)(1+γ2)(1+σ2)=P(i)×P(−i)
=(−2+3i)(−2−3i)
This is in the form (a+bi)(a−bi)=a2+b2.
=(−2)2+(3)2
=4+9
=13.
