Question
Question: If $\alpha, \beta, \gamma$ be the roots of $2x^3 + x^2 + x + 1 = 0$, find the value of: $(\frac{1}{...
If α,β,γ be the roots of 2x3+x2+x+1=0, find the value of:
(β31+γ31−α31)(γ31+α31−β31)(α31+β31−γ31)
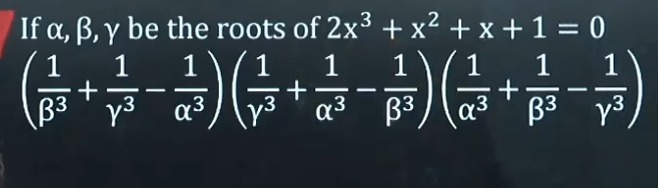
4
8
12
16
16
Solution
Here's how to solve this problem:
-
Define the original cubic equation 2x3+x2+x+1=0 with roots α,β,γ.
-
Form the reciprocal equation y3+y2+y+2=0 by substituting x=1/y. Its roots are A=1/α,B=1/β,C=1/γ.
-
Apply Vieta's formulas to the reciprocal equation:
- A+B+C=−1
- AB+BC+CA=1
- ABC=−2
-
Rewrite the given expression in terms of A,B,C: E=(B3+C3−A3)(C3+A3−B3)(A3+B3−C3).
-
Since A is a root of y3+y2+y+2=0, then A3=−A2−A−2. Similarly for B and C.
-
Calculate A3+B3+C3=−(A2+B2+C2)−(A+B+C)−6.
-
A2+B2+C2=(A+B+C)2−2(AB+BC+CA)=(−1)2−2(1)=−1.
-
Therefore, A3+B3+C3=−(−1)−(−1)−6=−4.
-
-
Let S3=A3+B3+C3=−4. The expression becomes (S3−2A3)(S3−2B3)(S3−2C3)=(−4−2A3)(−4−2B3)(−4−2C3)=−8(2+A3)(2+B3)(2+C3).
-
Substitute 2+A3=2+(−A2−A−2)=−A(A+1). Similarly for B and C.
-
The expression simplifies to −8[−A(A+1)][−B(B+1)][−C(C+1)]=8ABC(A+1)(B+1)(C+1).
-
Use P(y)=y3+y2+y+2=(y−A)(y−B)(y−C). Evaluate P(−1)=(−1−A)(−1−B)(−1−C)=−(A+1)(B+1)(C+1).
-
P(−1)=(−1)3+(−1)2+(−1)+2=1. So, −(A+1)(B+1)(C+1)=1⟹(A+1)(B+1)(C+1)=−1.
-
Substitute ABC=−2 and (A+1)(B+1)(C+1)=−1 into the simplified expression: 8(−2)(−1)=16.
