Question

If $\alpha, \beta, \gamma$ are the roots of $x^3 + 2x^2 + 3x + 2 = 0$, then the transformed equation whose roots are $\alpha(\beta + \gamma), \beta(\gamma + \alpha), \gamma(\alpha + \beta)$ is obtained by the substitution

Answer 1

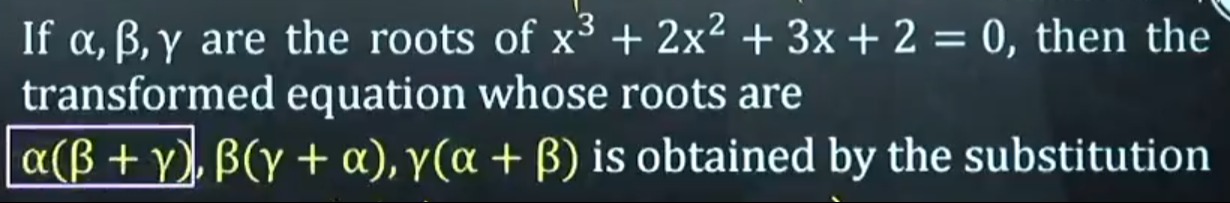
y = -x^2 - 2x

Answer 2

The given equation is $x^3 + 2x^2 + 3x + 2 = 0$. Let its roots be $\alpha, \beta, \gamma$.

From Vieta's formulas, we have:

1. Sum of roots: $\alpha + \beta + \gamma = -2$

2. Sum of products of roots taken two at a time: $\alpha\beta + \beta\gamma + \gamma\alpha = 3$

3. Product of roots: $\alpha\beta\gamma = -2$

We need to find the transformed equation whose roots are $y_1 = \alpha(\beta + \gamma)$, $y_2 = \beta(\gamma + \alpha)$, $y_3 = \gamma(\alpha + \beta)$.

Let's express a general new root, say $y_1$, in terms of $\alpha$ and the sum of roots. We know that $\beta + \gamma = (\alpha + \beta + \gamma) - \alpha$. Substitute the value of $\alpha + \beta + \gamma$ from Vieta's formulas: $\beta + \gamma = -2 - \alpha$.

Now, substitute this into the expression for $y_1$: $y_1 = \alpha(-2 - \alpha)$ $y_1 = -2\alpha - \alpha^2$

Similarly, for the other roots: $y_2 = \beta(-2 - \beta) = -2\beta - \beta^2$ $y_3 = \gamma(-2 - \gamma) = -2\gamma - \gamma^2$

This shows that the relationship between the new root $y$ and the old root $x$ is given by the substitution: $y = -x^2 - 2x$

To verify this, we can find the transformed equation. From the substitution, we have $x^2 + 2x = -y$. The original equation is $x^3 + 2x^2 + 3x + 2 = 0$. We can rewrite it as $x(x^2 + 2x) + 3x + 2 = 0$. Substitute $x^2 + 2x = -y$ into this equation: $x(-y) + 3x + 2 = 0$ $-xy + 3x + 2 = 0$ $x(3 - y) = -2$ $x = \frac{-2}{3 - y} = \frac{2}{y - 3}$

Now, substitute this expression for $x$ back into $x^2 + 2x = -y$: $\left(\frac{2}{y - 3}\right)^2 + 2\left(\frac{2}{y - 3}\right) = -y$ $\frac{4}{(y - 3)^2} + \frac{4}{y - 3} = -y$ Multiply the entire equation by $(y - 3)^2$ to clear the denominators: $4 + 4(y - 3) = -y(y - 3)^2$ $4 + 4y - 12 = -y(y^2 - 6y + 9)$ $4y - 8 = -y^3 + 6y^2 - 9y$ Move all terms to one side to form a standard polynomial equation: $y^3 - 6y^2 + 9y + 4y - 8 = 0$ $y^3 - 6y^2 + 13y - 8 = 0$ This is the transformed equation. The substitution used to obtain it is $y = -x^2 - 2x$.