Question

If $\alpha$, $\beta$, $\gamma$ are the roots of equation $x^3=x^2+1$, then find the equation whose roots are $\alpha^2 + \beta^3 + \gamma^4$, $\alpha^4 + \beta^2 + \gamma^3$, $\gamma^2 + \alpha^3 + \beta^4$.

Answer 1

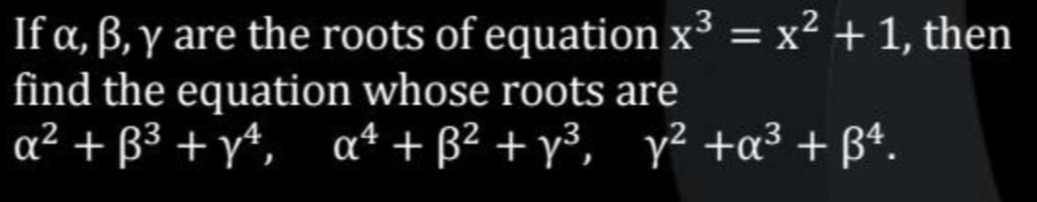
y^3 - 10y^2 + 33y - 37 = 0

Answer 2

Let the given equation be $P(x) = x^3 - x^2 - 1 = 0$. Let its roots be $\alpha, \beta, \gamma$.

From Vieta's formulas:

1. Sum of roots: $\alpha + \beta + \gamma = -(-1)/1 = 1$
2. Sum of products of roots taken two at a time: $\alpha\beta + \beta\gamma + \gamma\alpha = 0/1 = 0$
3. Product of roots: $\alpha\beta\gamma = -(-1)/1 = 1$

Since $\alpha, \beta, \gamma$ are roots of $x^3 - x^2 - 1 = 0$, they satisfy the equation: $\alpha^3 = \alpha^2 + 1$ $\beta^3 = \beta^2 + 1$ $\gamma^3 = \gamma^2 + 1$

We can also find expressions for higher powers: $\alpha^4 = \alpha \cdot \alpha^3 = \alpha(\alpha^2 + 1) = \alpha^3 + \alpha = (\alpha^2 + 1) + \alpha = \alpha^2 + \alpha + 1$ Similarly, $\beta^4 = \beta^2 + \beta + 1$ $\gamma^4 = \gamma^2 + \gamma + 1$

The new roots are given as: $y_1 = \alpha^2 + \beta^3 + \gamma^4$ $y_2 = \alpha^4 + \beta^2 + \gamma^3$ $y_3 = \gamma^2 + \alpha^3 + \beta^4$

Let's substitute the simplified power expressions into the new roots: For $y_1$: $y_1 = \alpha^2 + (\beta^2 + 1) + (\gamma^2 + \gamma + 1)$ $y_1 = \alpha^2 + \beta^2 + \gamma^2 + \gamma + 2$

For $y_2$: $y_2 = (\alpha^2 + \alpha + 1) + \beta^2 + (\gamma^2 + 1)$ $y_2 = \alpha^2 + \beta^2 + \gamma^2 + \alpha + 2$

For $y_3$ (rearranging terms for consistency: $\alpha^3 + \beta^4 + \gamma^2$): $y_3 = (\alpha^2 + 1) + (\beta^2 + \beta + 1) + \gamma^2$ $y_3 = \alpha^2 + \beta^2 + \gamma^2 + \beta + 2$

Now, let's calculate the sum of squares of the original roots, $S_2 = \alpha^2 + \beta^2 + \gamma^2$: $S_2 = (\alpha + \beta + \gamma)^2 - 2(\alpha\beta + \beta\gamma + \gamma\alpha)$ Using Vieta's formulas: $S_2 = (1)^2 - 2(0) = 1$

Substitute $S_2 = 1$ into the expressions for $y_1, y_2, y_3$: $y_1 = 1 + \gamma + 2 = \gamma + 3$ $y_2 = 1 + \alpha + 2 = \alpha + 3$ $y_3 = 1 + \beta + 2 = \beta + 3$

So, the new roots are $\alpha+3$, $\beta+3$, and $\gamma+3$. If the roots of the new equation are $y$, and the roots of the original equation are $x$, then $y = x+3$. This implies $x = y-3$. Substitute $x = y-3$ into the original equation $x^3 - x^2 - 1 = 0$: $(y-3)^3 - (y-3)^2 - 1 = 0$

Expand the terms: $(y-3)^3 = y^3 - 3(y^2)(3) + 3(y)(3^2) - 3^3 = y^3 - 9y^2 + 27y - 27$ $(y-3)^2 = y^2 - 2(y)(3) + 3^2 = y^2 - 6y + 9$

Substitute these expansions back into the equation: $(y^3 - 9y^2 + 27y - 27) - (y^2 - 6y + 9) - 1 = 0$ $y^3 - 9y^2 + 27y - 27 - y^2 + 6y - 9 - 1 = 0$

Combine like terms: $y^3 + (-9-1)y^2 + (27+6)y + (-27-9-1) = 0$ $y^3 - 10y^2 + 33y - 37 = 0$

This is the equation whose roots are $\alpha+3, \beta+3, \gamma+3$.