Question

If $\alpha$, $\beta$, $\gamma$ are the roots of equation $x^3 = x^2 + 1$, then find the equation whose roots are $\alpha^2 + \beta^3 + \gamma^4$, $\alpha^4 + \beta^2 + \gamma^3$, $\gamma^2 + \alpha^3 + \beta^4$.

Answer 1

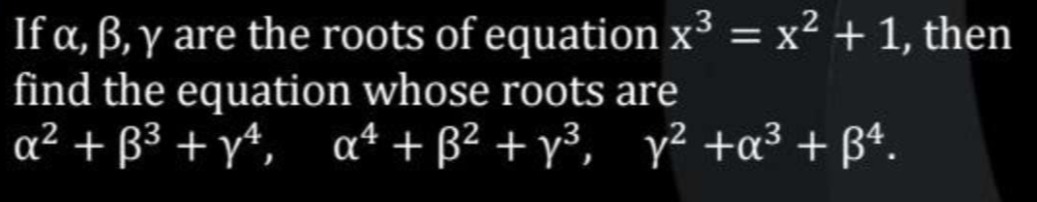
x^3 - 10x^2 + 33x - 37 = 0

Answer 2

The given equation is $x^3 = x^2 + 1$. Its roots are $\alpha, \beta, \gamma$.

From this equation, we can derive relations for higher powers of the roots:

1. $x^3 = x^2 + 1$
2. $x^4 = x \cdot x^3 = x(x^2+1) = x^3+x$. Substituting $x^3=x^2+1$ again, we get $x^4 = (x^2+1)+x = x^2+x+1$.

From Vieta's formulas for $x^3 - x^2 - 1 = 0$:

$\alpha + \beta + \gamma = 1$

$\alpha\beta + \beta\gamma + \gamma\alpha = 0$

$\alpha\beta\gamma = 1$

Now, let's find the sum of squares of the roots:

$\alpha^2 + \beta^2 + \gamma^2 = (\alpha+\beta+\gamma)^2 - 2(\alpha\beta+\beta\gamma+\gamma\alpha) = (1)^2 - 2(0) = 1$.

The roots of the new equation are $y_1 = \alpha^2 + \beta^3 + \gamma^4$, $y_2 = \alpha^4 + \beta^2 + \gamma^3$, $y_3 = \gamma^2 + \alpha^3 + \beta^4$.

Let's simplify these expressions using the relations derived:

For $y_1$:

$y_1 = \alpha^2 + \beta^3 + \gamma^4$

Substitute $\beta^3 = \beta^2+1$ and $\gamma^4 = \gamma^2+\gamma+1$:

$y_1 = \alpha^2 + (\beta^2+1) + (\gamma^2+\gamma+1)$

$y_1 = (\alpha^2+\beta^2+\gamma^2) + \gamma + 2$

Since $\alpha^2+\beta^2+\gamma^2 = 1$:

$y_1 = 1 + \gamma + 2 = \gamma + 3$

Similarly for $y_2$:

$y_2 = \alpha^4 + \beta^2 + \gamma^3$

Substitute $\alpha^4 = \alpha^2+\alpha+1$ and $\gamma^3 = \gamma^2+1$:

$y_2 = (\alpha^2+\alpha+1) + \beta^2 + (\gamma^2+1)$

$y_2 = (\alpha^2+\beta^2+\gamma^2) + \alpha + 2$

$y_2 = 1 + \alpha + 2 = \alpha + 3$

And for $y_3$:

$y_3 = \gamma^2 + \alpha^3 + \beta^4$

Substitute $\alpha^3 = \alpha^2+1$ and $\beta^4 = \beta^2+\beta+1$:

$y_3 = \gamma^2 + (\alpha^2+1) + (\beta^2+\beta+1)$

$y_3 = (\alpha^2+\beta^2+\gamma^2) + \beta + 2$

$y_3 = 1 + \beta + 2 = \beta + 3$

So, the roots of the new equation are $\alpha+3, \beta+3, \gamma+3$.

Let $y$ be a root of the new equation. Then $y = x+3$, which implies $x = y-3$.

Substitute $x=y-3$ into the original equation $x^3 - x^2 - 1 = 0$:

$(y-3)^3 - (y-3)^2 - 1 = 0$

Expand the terms:

$(y-3)^3 = y^3 - 3(y^2)(3) + 3(y)(3^2) - 3^3 = y^3 - 9y^2 + 27y - 27$

$(y-3)^2 = y^2 - 2(y)(3) + 3^2 = y^2 - 6y + 9$

Substitute these expansions back into the equation:

$(y^3 - 9y^2 + 27y - 27) - (y^2 - 6y + 9) - 1 = 0$

$y^3 - 9y^2 + 27y - 27 - y^2 + 6y - 9 - 1 = 0$

Combine like terms:

$y^3 + (-9-1)y^2 + (27+6)y + (-27-9-1) = 0$

$y^3 - 10y^2 + 33y - 37 = 0$

This is the equation whose roots are $\alpha+3, \beta+3, \gamma+3$.