Question

If $\alpha ,\beta ,\gamma$ are real roots of the equation ${x^3} - 3p{x^2} + 3qx - 1 = 0$ then the centroid of the triangle, whose vertices are $\left( {\alpha ,\dfrac{1}{\alpha }} \right),\left( {\beta ,\dfrac{1}{\beta }} \right)and\left( {\gamma ,\dfrac{1}{\gamma }} \right)$ is?

Answer 1

Given equation is a cubic equation. Using the conditions of the roots the cubic equation and centroid formula we can calculate the coordinates of the centroid.

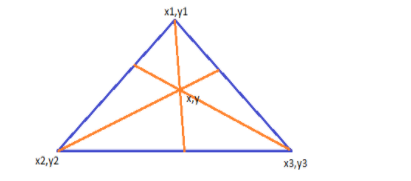
In general given above is a triangle with its vertices. So using centroid formula coordinates of centroid are
$\left( {x,y} \right) = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$

Complete step-by-step answer:
Given that,
${x^3} - 3p{x^2} + 3qx - 1 = 0$
It is a cubic equation.
We know that for a quadratic equation given above $\alpha ,\beta ,\gamma$ are the roots.
Sum of the roots is equal to the negative of the ratio of coefficients of second term to first term.
Here the coefficient of first term is 1, of second term is -3p, and third term is +3q and of last term is -1.
Thus we conclude that,
$\alpha + \beta + \gamma = - (\dfrac{{ - 3p}}{1}) = 3p$
The sum of products of roots is equal to the ratio of coefficients of third term to first term.
$\alpha \beta + \beta \gamma + \gamma \alpha = \dfrac{{3q}}{1} = 3q$
The product of the roots is equal to the negative of ratio of coefficients of last term to first term
$\alpha \beta \gamma = - \dfrac{{( - 1)}}{1} = 1$
Now we will use centroid formula,
$\left( {x,y} \right) = \left( {\dfrac{{{x_1} + {x_2} + {x_3}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3}} \right)$
The vertices of the triangle given
$\left( {\alpha ,\dfrac{1}{\alpha }} \right),\left( {\beta ,\dfrac{1}{\beta }} \right)and\left( {\gamma ,\dfrac{1}{\gamma }} \right)$ .
Let the vertices of the centroid be $(x,y)$.
$\Rightarrow (x,y) = \left( {\dfrac{{\alpha + \beta + \gamma }}{3},\dfrac{{\dfrac{1}{\alpha } + \dfrac{1}{\beta } + \dfrac{1}{\gamma }}}{3}} \right)$
$\Rightarrow (x,y) = \left( {\dfrac{{\alpha + \beta + \gamma }}{3},\dfrac{{\beta \gamma + \alpha \gamma + \alpha \beta }}{{3\alpha \beta \gamma }}} \right)$
Now substitute the values that we have obtained between the roots of the Equation and coefficients of the centroid of the triangle.

$$\Rightarrow (x,y) = \left( {\dfrac{{3p}}{3},\dfrac{{3q}}{{3 \times 1}}} \right) \\\ \Rightarrow (x,y) = \left( {p,q} \right) \\\$$

Thus the centroid of the triangle is $\left( {p,q} \right)$.

Note: Don’t get confused between the roots of the equation and vertices of the triangle here because both are mentioned with the same symbol. First obtain the relation between roots of the equation and then replace them with coefficients of the equation.
$a{x^3} + b{x^2} + cx + d = 0$ is the general form of the cubic equation.