Solveeit Logo
Login

Question

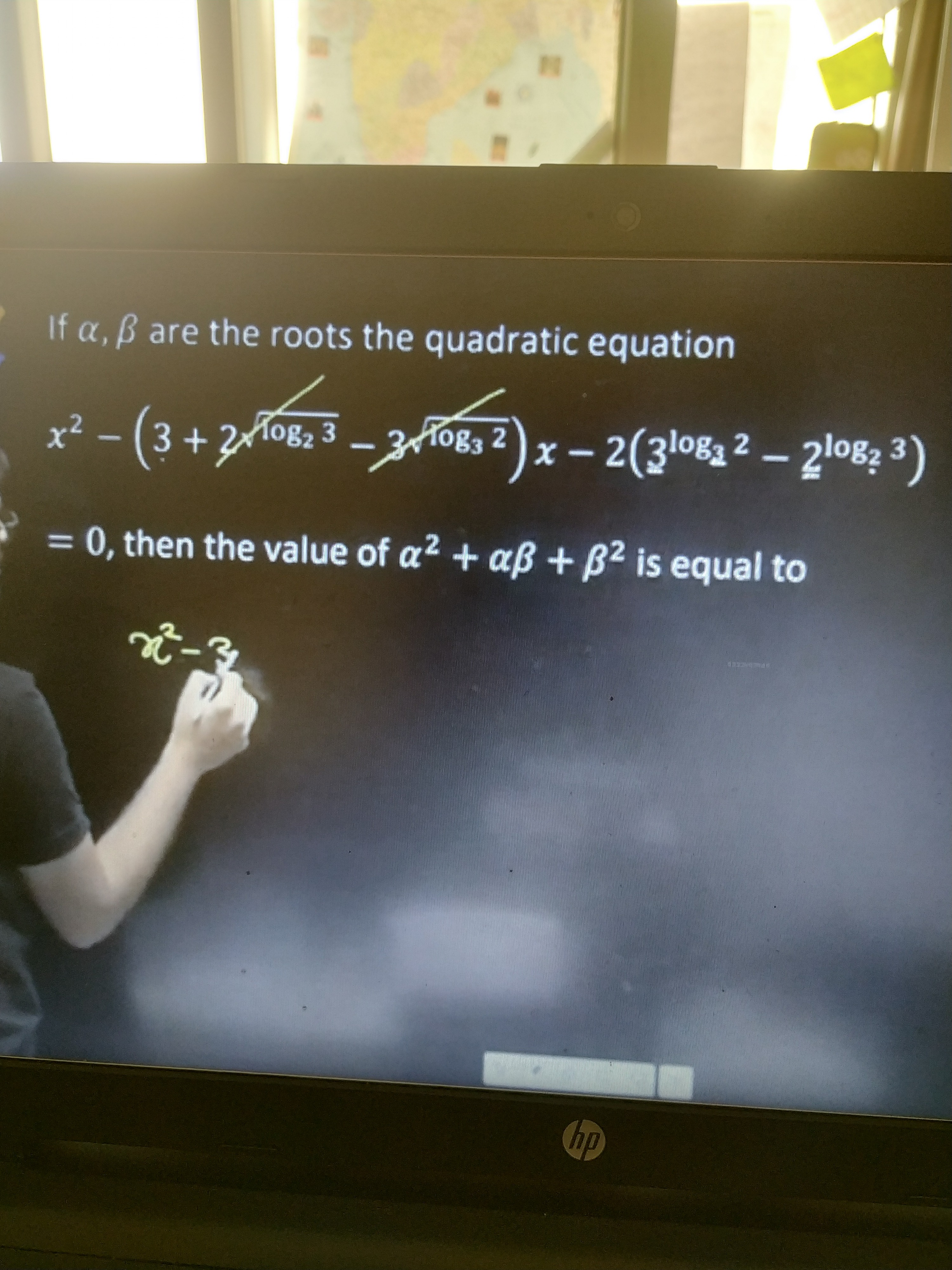
Question: If $\alpha, \beta$ are the roots the quadratic equation $x^2 - (3 + 2^{\log_2 3} - 3^{\log_3 2})x - ...

If α,β\alpha, \beta are the roots the quadratic equation x2−(3+2log⁡23−3log⁡32)x−2(3log⁡32−2log⁡23)x^2 - (3 + 2^{\log_2 3} - 3^{\log_3 2})x - 2(3^{\log_3 2} - 2^{\log_2 3}) = 0, then the value of α2+αβ+β2\alpha^2 + \alpha\beta + \beta^2 is equal to

Answer

14

Explanation

Solution

The given quadratic equation is x2−(3+2log⁡23−3log⁡32)x−2(3log⁡32−2log⁡23)=0x^2 - (3 + 2^{\log_2 3} - 3^{\log_3 2})x - 2(3^{\log_3 2} - 2^{\log_2 3}) = 0.

We use the property of logarithms alog⁡ab=ba^{\log_a b} = b. So, 2log⁡23=32^{\log_2 3} = 3 and 3log⁡32=23^{\log_3 2} = 2.

Substitute these values into the equation:

The coefficient of xx is −(3+2log⁡23−3log⁡32)=−(3+3−2)=−(6−2)=−4-(3 + 2^{\log_2 3} - 3^{\log_3 2}) = -(3 + 3 - 2) = -(6 - 2) = -4. The constant term is −2(3log⁡32−2log⁡23)=−2(2−3)=−2(−1)=2-2(3^{\log_3 2} - 2^{\log_2 3}) = -2(2 - 3) = -2(-1) = 2.

The quadratic equation is x2−4x+2=0x^2 - 4x + 2 = 0.

Let α\alpha and β\beta be the roots of this equation.

According to Vieta's formulas, the sum of the roots is α+β=−coefficient of xcoefficient of x2=−−41=4\alpha + \beta = -\frac{\text{coefficient of } x}{\text{coefficient of } x^2} = -\frac{-4}{1} = 4. The product of the roots is αβ=constant termcoefficient of x2=21=2\alpha\beta = \frac{\text{constant term}}{\text{coefficient of } x^2} = \frac{2}{1} = 2.

We are asked to find the value of α2+αβ+β2\alpha^2 + \alpha\beta + \beta^2. We can rewrite this expression using the sum and product of the roots.

α2+αβ+β2=(α2+2αβ+β2)−αβ=(α+β)2−αβ\alpha^2 + \alpha\beta + \beta^2 = (\alpha^2 + 2\alpha\beta + \beta^2) - \alpha\beta = (\alpha + \beta)^2 - \alpha\beta.

Substitute the values of α+β\alpha + \beta and αβ\alpha\beta:

α2+αβ+β2=(4)2−2=16−2=14\alpha^2 + \alpha\beta + \beta^2 = (4)^2 - 2 = 16 - 2 = 14.