Question

If $\alpha$, $\beta$ are roots of the equation $(3x + 2)^2 + p(3x + 2) + q = 0$, then roots of $x^2 + px + q = 0$ are

Answer 1

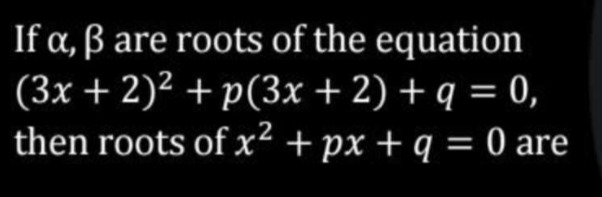
3\alpha + 2, 3\beta + 2

Answer 2

Let the given equation be $(3x + 2)^2 + p(3x + 2) + q = 0$ Let $y = 3x + 2$. Substituting this into the equation, we get a new quadratic equation in terms of $y$: $y^2 + py + q = 0$ We are given that $\alpha$ and $\beta$ are the roots of the original equation $(3x + 2)^2 + p(3x + 2) + q = 0$. This means that when $x = \alpha$, the equation holds true: $(3\alpha + 2)^2 + p(3\alpha + 2) + q = 0$ Comparing this with $y^2 + py + q = 0$, we can see that $y_1 = 3\alpha + 2$ is a root of the equation $y^2 + py + q = 0$.

Similarly, when $x = \beta$, the equation holds true: $(3\beta + 2)^2 + p(3\beta + 2) + q = 0$ This implies that $y_2 = 3\beta + 2$ is also a root of the equation $y^2 + py + q = 0$.

So, the roots of the equation $y^2 + py + q = 0$ are $3\alpha + 2$ and $3\beta + 2$.

The question asks for the roots of the equation $x^2 + px + q = 0$. This equation is identical in form to $y^2 + py + q = 0$, just with the variable $x$ instead of $y$. Therefore, the roots of $x^2 + px + q = 0$ are the same as the roots of $y^2 + py + q = 0$. Hence, the roots of $x^2 + px + q = 0$ are $3\alpha + 2$ and $3\beta + 2.