Question

If $\alpha$ and $\beta$ are the two real values of x which satisfy the equation $\frac{4x^2+15x+17}{x^2+4x+12} = \frac{5x^2+16x+18}{2x^2+5x+13}$, then which of the following option(s) is(are) CORRECT?

Answer 1

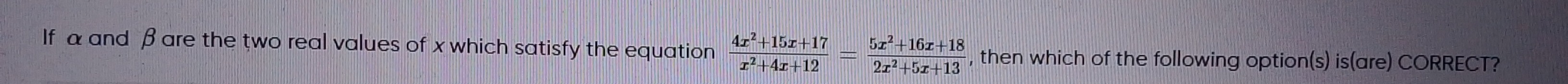
Multiple properties can be derived for $\alpha$ and $\beta$ as follows: $\alpha+\beta = -11/3$, $\alpha\beta = 5/3$, $\alpha^2+\beta^2 = 91/9$, and both roots are negative.

Answer 2

The given equation is: $\frac{4x^2+15x+17}{x^2+4x+12} = \frac{5x^2+16x+18}{2x^2+5x+13}$

Let's analyze the numerators and denominators. Consider the difference between the numerator and denominator for the first fraction: $(4x^2+15x+17) - (x^2+4x+12) = 3x^2+11x+5$ Consider the difference between the numerator and denominator for the second fraction: $(5x^2+16x+18) - (2x^2+5x+13) = 3x^2+11x+5$ Notice that both differences are the same. Let $P(x) = 3x^2+11x+5$. Let $D_1 = x^2+4x+12$ and $D_2 = 2x^2+5x+13$. Then the equation can be rewritten as: $\frac{D_1+P(x)}{D_1} = \frac{D_2+P(x)}{D_2}$ $1 + \frac{P(x)}{D_1} = 1 + \frac{P(x)}{D_2}$ $\frac{P(x)}{D_1} = \frac{P(x)}{D_2}$ This equation holds if either $P(x) = 0$ or $D_1 = D_2$.

Case 1: $P(x) = 0$ $3x^2+11x+5 = 0$ The roots of this quadratic equation are given by the quadratic formula: $x = \frac{-11 \pm \sqrt{11^2 - 4(3)(5)}}{2(3)}$ $x = \frac{-11 \pm \sqrt{121 - 60}}{6}$ $x = \frac{-11 \pm \sqrt{61}}{6}$ These are two distinct real roots. Let these be $\alpha$ and $\beta$. We must check if the denominators $D_1$ and $D_2$ are non-zero for these values of $x$. For $D_1 = x^2+4x+12$, the discriminant is $\Delta_1 = 4^2 - 4(1)(12) = 16 - 48 = -32 < 0$. Since the leading coefficient (1) is positive, $D_1 > 0$ for all real $x$. For $D_2 = 2x^2+5x+13$, the discriminant is $\Delta_2 = 5^2 - 4(2)(13) = 25 - 104 = -79 < 0$. Since the leading coefficient (2) is positive, $D_2 > 0$ for all real $x$. Thus, the denominators are never zero, and these two real roots are valid solutions to the original equation.

Case 2: $D_1 = D_2$ $x^2+4x+12 = 2x^2+5x+13$ Rearranging the terms: $0 = (2x^2-x^2) + (5x-4x) + (13-12)$ $x^2+x+1 = 0$ The discriminant of this quadratic equation is $\Delta = 1^2 - 4(1)(1) = 1 - 4 = -3 < 0$. Since the discriminant is negative, this equation has no real roots.

Therefore, the two real values of $x$, $\alpha$ and $\beta$, which satisfy the given equation are the roots of $3x^2+11x+5=0$.

Using Vieta's formulas for the quadratic equation $3x^2+11x+5=0$:

1. Sum of roots: $\alpha + \beta = -\frac{11}{3}$
2. Product of roots: $\alpha \beta = \frac{5}{3}$
3. Sum of squares of roots: $\alpha^2 + \beta^2 = (\alpha+\beta)^2 - 2\alpha\beta = \left(-\frac{11}{3}\right)^2 - 2\left(\frac{5}{3}\right) = \frac{121}{9} - \frac{10}{3} = \frac{121 - 30}{9} = \frac{91}{9}$
4. Difference of roots: $|\alpha - \beta| = \frac{\sqrt{\Delta}}{|A|} = \frac{\sqrt{61}}{3}$
5. Sign of roots: Since $\alpha\beta = 5/3 > 0$, both roots have the same sign. Since $\alpha+\beta = -11/3 < 0$, both roots must be negative.

The question asks which of the following options are correct. Since no options are provided, we list the properties derived.

The final answer is $\boxed{\text{Multiple properties can be derived for } \alpha \text{ and } \beta \text{ as follows: } \alpha+\beta = -11/3, \alpha\beta = 5/3, \alpha^2+\beta^2 = 91/9, \text{ and both roots are negative.}}$

Explanation of the solution: The key step is to observe that the difference between the numerator and denominator is the same for both fractions. Let this common difference be $P(x) = 3x^2+11x+5$. The equation simplifies to $\frac{D_1+P(x)}{D_1} = \frac{D_2+P(x)}{D_2}$, which means $1+\frac{P(x)}{D_1} = 1+\frac{P(x)}{D_2}$, leading to $\frac{P(x)}{D_1} = \frac{P(x)}{D_2}$. This implies either $P(x)=0$ or $D_1=D_2$. The equation $P(x)=0$ gives $3x^2+11x+5=0$, whose real roots are $\alpha = \frac{-11 + \sqrt{61}}{6}$ and $\beta = \frac{-11 - \sqrt{61}}{6}$. The denominators $D_1=x^2+4x+12$ and $D_2=2x^2+5x+13$ are always positive (their discriminants are negative and leading coefficients are positive), so they are never zero. The equation $D_1=D_2$ gives $x^2+x+1=0$, which has no real roots as its discriminant is negative. Therefore, $\alpha$ and $\beta$ are the roots of $3x^2+11x+5=0$. From Vieta's formulas:

• Sum of roots: $\alpha + \beta = -11/3$.
• Product of roots: $\alpha \beta = 5/3$.
• Sum of squares: $\alpha^2 + \beta^2 = (\alpha+\beta)^2 - 2\alpha\beta = (-11/3)^2 - 2(5/3) = 121/9 - 10/3 = 91/9$.
• Both roots are negative because their product is positive and their sum is negative.