Question
Question: If $\alpha$ and $\beta$ are the roots of the equation 2x (2x + 1) = 1, then $\beta$ is equal to...
If α and β are the roots of the equation 2x (2x + 1) = 1, then β is equal to
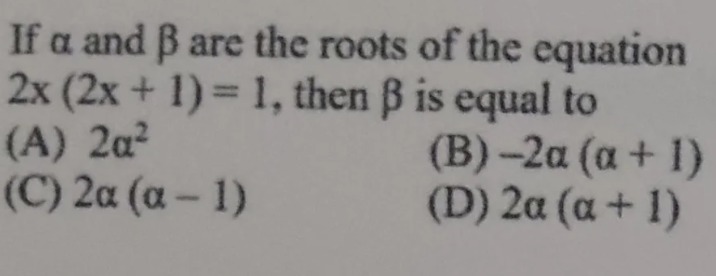
2α2
−2α(α+1)
2α(α−1)
2α(α+1)
(B)
Solution
The given equation is 2x(2x+1)=1. Expanding this, we get 4x2+2x=1. Rearranging into the standard quadratic form ax2+bx+c=0, we have 4x2+2x−1=0.
Let α and β be the roots of this equation. According to Vieta's formulas, the sum of the roots is α+β=−ab and the product of the roots is αβ=ac. For the equation 4x2+2x−1=0, we have a=4, b=2, and c=−1. The sum of the roots is α+β=−42=−21. The product of the roots is αβ=4−1=−41.
From the sum of roots, we can express β in terms of α: β=−21−α.
Since α is a root of the equation 4x2+2x−1=0, it must satisfy the equation: 4α2+2α−1=0. From this equation, we can express 4α2 or 2α2 in terms of α: 4α2=1−2α and 2α2=21−2α=21−α.
Now let's evaluate the given options using the relation 2α2=21−α and compare them with the expression for β, which is −21−α.
(A) 2α2=21−α. This is not equal to −21−α. (B) −2α(α+1)=−2α2−2α. Substitute 2α2=21−α: −2α2−2α=−(21−α)−2α=−21+α−2α=−21−α. This matches the expression for β. (C) 2α(α−1)=2α2−2α. Substitute 2α2=21−α: 2α2−2α=(21−α)−2α=21−3α. This is not equal to −21−α. (D) 2α(α+1)=2α2+2α. Substitute 2α2=21−α: 2α2+2α=(21−α)+2α=21+α. This is not equal to −21−α.
Thus, option (B) is the correct expression for β in terms of α.
