Question
Question: If $\alpha$, $\alpha + 1$ are the roots of the equation $x^2 + nx + (n + 5) = 0$ then the non-negati...
If α, α+1 are the roots of the equation x2+nx+(n+5)=0 then the non-negative value of n is equal to
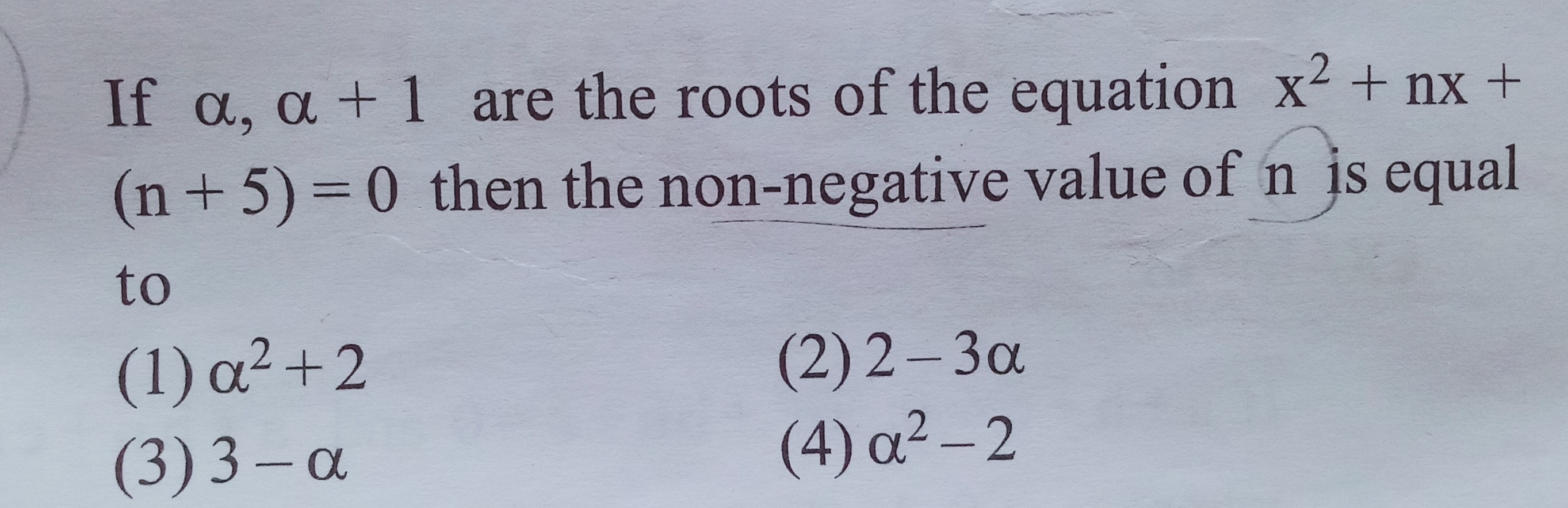
α2+2
2−3α
3−α
α2−2
3−α
Solution
The given quadratic equation is x2+nx+(n+5)=0. Let the roots be r1=α and r2=α+1.
According to Vieta's formulas:
Sum of roots: r1+r2=−1n
α+(α+1)=−n
2α+1=−n
n=−(2α+1) (Equation 1)
Product of roots: r1⋅r2=1n+5
α(α+1)=n+5
α2+α=n+5 (Equation 2)
Substitute Equation 1 into Equation 2:
α2+α=−(2α+1)+5
α2+α=−2α−1+5
α2+α=−2α+4
α2+3α−4=0
Solve the quadratic equation for α:
(α+4)(α−1)=0
This gives two possible values for α:
α=−4 or α=1.
Now, find the corresponding value of n for each value of α using Equation 1 (n=−(2α+1)).
Case 1: α=−4
n=−(2(−4)+1)=−(−8+1)=−(−7)=7. In this case, the roots are α=−4 and α+1=−3. The equation is x2+7x+(7+5)=0⟹x2+7x+12=0. The roots of x2+7x+12=0 are indeed −3 and −4. The value of n is 7, which is non-negative.
Case 2: α=1
n=−(2(1)+1)=−(2+1)=−3. In this case, the roots are α=1 and α+1=2. The equation is x2−3x+(−3+5)=0⟹x2−3x+2=0. The roots of x2−3x+2=0 are indeed 1 and 2. The value of n is -3, which is negative.
The question asks for the non-negative value of n. From the two cases, the non-negative value of n is 7. This non-negative value of n=7 occurs when α=−4.
Now we need to find which of the given options is equal to 7, using the value of α that corresponds to n=7, which is α=−4.
Let's evaluate each option with α=−4:
(1) α2+2=(−4)2+2=16+2=18.
(2) 2−3α=2−3(−4)=2+12=14.
(3) 3−α=3−(−4)=3+4=7.
(4) α2−2=(−4)2−2=16−2=14.
Option (3) evaluates to 7, which is the non-negative value of n.
