Question

If acceleration of $A$ is $2\,{m}/{{{s}^{2}}}$ which is smaller than acceleration of $B$ then the value of frictional force applied by $B$ on $A$ is:

Answer 1

In order to answer the above question, we will draw a free body diagram and try to understand the forces acting on the body. We will then use the conservation of forces and write the equation of balancing the forces. Finally, we will calculate the frictional force acting on $A$.

Formula used:
Force = mass $\times$ acceleration
$f=ma$

Complete step by step answer:
First of all we will redraw the diagram given in the question and try to understand the question properly.

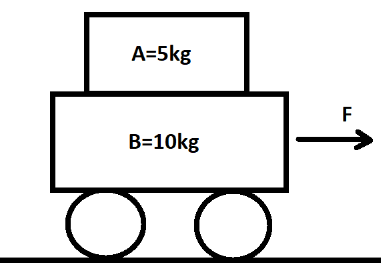
As we can conclude from the figure, a block named $B$ having mass $10\,kg$ is moving with some acceleration in the positive(x) direction. Another block having mass $5\,kg$ is placed on top of $B$ is also moving with an acceleration of $2\,{m}/{{{s}^{2}}}$ in the positive(x) direction.

It is given that the acceleration of $A$ is less than the acceleration of $B$. But as we know that $A$ is placed on $B$, so they should have the same acceleration in the positive(x) direction. Therefore, we can conclude that $A$ is also moving in the negative(x) direction with some acceleration with respect to $B$ and is making it slower than $B$.

In order to understand the situation properly, we will draw a simple free body diagram for $A$.

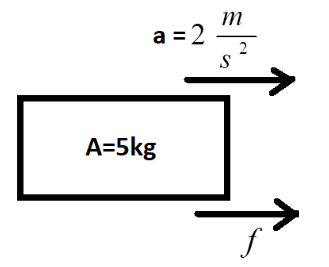
The above condition can also be examined as there is relative motion between the blocks as $A$ slides on the block $B$ with an acceleration of $2\,{m}/{{{s}^{2}}}$. As a result, the block is under the action of a maximum frictional force, which provides it with the acceleration of $2\,{m}/{{{s}^{2}}}$. Writing the equation of forces or balancing the forces acting on the box, we get
$mg=N$ …(1)
Here, both the forces have equal magnitude and opposite directions, so they cancel out each other. And the frictional force on $A$ is equal to the force due to the acceleration generated by the friction. Therefore, $f=ma$
$f=(5kg)\left( 2\dfrac{m}{{{s}^{2}}} \right) \\\ \Rightarrow f=10N \\\$
Therefore, the frictional force acting on $A$ is $f=10\,N$.

Note: It is very important to keep in mind the relative motion of $A$ and $B$ with respect to each other and also the relative motion with respect to the ground. It is also important to notice in the above solution that the force due to friction in this problem is acting in the positive(x) direction and is along the motion of the object which is in contrast to the solutions of many other problems related to friction.