Question
Question: If ABCDEF is regular hexagon and O is center also \(\overrightarrow { AB } +\overrightarrow { AC } +...
If ABCDEF is regular hexagon and O is center also AB+AC+AD+AE+AF=tAO then find the value of t.
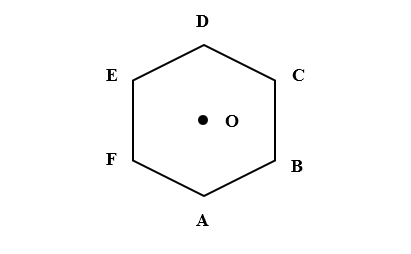
A. 3
B. 2
C. 6
D. 8
Solution
To solve this question, first draw the vectors asked in the question in the given diagram. Then use the concepts of vector algebra. Use the vector addition through triangle law of vector addition in which two vectors to be added is represented as a side of triangle and resultant vector is the third side of the triangle. Using this find the terms of the expression given in the question and thus, find the value of t.
Complete answer:
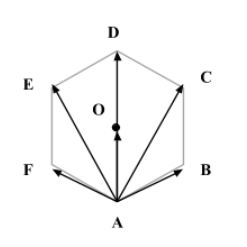
Given: AB+AC+AD+AE+AF=tAO …(1)
From the figure drawn above, we can see AC is a resultant vector of AO and AB.
⇒AC=AB+AO …(2)
Similarly, AE is a resultant vector of AO and AF.
⇒AE=AF+AO …(3)
Substituting equation. (2) and (3) on the left-hand side of the equation. (1} we get,
L.H.S=AB+AB+AO+AD+AF+AO+AF
⇒L.H.S=2AB+2AO+2AF+AD …(4)
In the figure, we can see AD=2AO
Substituting this value in the equation. (4) we get,
L.H.S=2AB+2AO+2AF+2AO
⇒L.H.S=2AB+4AO+2AF
⇒L.H.S=2(AB+AF)+4AO …(5)
From the figure drawn above, we can infer that AO is a resultant vector of AB and AF.
⇒AO=AB+AF …(6)
Substituting equation. (6) in equation. (5) we get,
L.H.S=2AO+4AO
⇒L.H.S=6AO …(7)
Now, comparing equations. (7} with equation. (1) we get,
t=6
Hence, the value of t is 6.
Note:
To solve these types of questions, students must be aware of the use of vectors. They should also know the triangle law of vector addition. Major part of this problem could be solved without much calculation and just by using the symmetry of geometrical shape given. But it would make the problem trivial. So, it is important to solve this problem using basic principles of vector and not overcomplicate the problem.
