Question

If $ABCDEF$ is a regular hexagon with $AB = \vec a$ and $BC = \vec b$ then $CE$ equals :
A.$\vec b - \vec a$
B.$- \vec b$
C.$\vec b - 2\vec a$
D.None of these

Answer 1

This question utilises the laws of vector addition and multiple properties of vectors that need to be remembered to solve this question. We approach or begin this question by marking the vectors on a regular hexagon and solve for different sides until we get the diagonal that the question is asking for. We will need to remember the properties of the isosceles triangle that is a part of a regular hexagon.

Complete step by step solution:

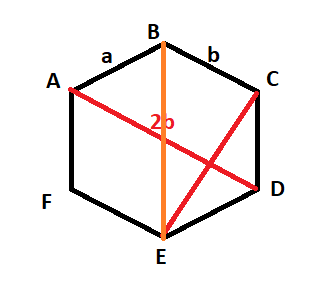
In the question, two vectors have been given. They are both adjacent vectors, that is
$AB = \vec a$ and $BC = \vec b$ .
The question asks for the body diagonal that passes through B and E.
That is, $CE = ?$
We can see that $ABCD$ is part of an equilateral triangle with $AD$ as the base and $BC$ passing through the midpoints of the other two sides. This property gives the conclusion that the base is twice the length of the line passing through the midpoints of the sides.
Therefore,
$AD = 2\vec b$
Using the laws of vector addition of a polygon,
$AD = AB + BC + CD$
$\Rightarrow 2\vec b = \vec a + \vec b + CD$
$CD = \vec b - \vec a$
Since $BE$ is twice the length as $CD$ and has same directions, that is parallel direction, therefore,
$BE = 2CD$
$\Rightarrow BE = 2\vec b - 2\vec a$
Again using triangle law of vector addition,
$BE = BC + CE$
$CE = BE - BC = 2\vec b - 2\vec a - b$
$\Rightarrow CE = \vec b - 2\vec a$
Therefore the correct option for this question is $\left( c \right)\vec b - 2\vec a$

Note:
This question has multiple ways to solve it since any amount can be solved before we get the vector we require. Many sides can all be clubbed together and many diagonals can be calculated simply to get the diagonal we need. It’s all about solving the question in as few steps as possible to make it fast and avoid any silly mistakes.