Solveeit Logo
Login

Question

Question: If ABCD is a quadrilateral such that \( \overline{AB}=2\widehat{i}-3\widehat{j}+\widehat{k} \) , \( ...

If ABCD is a quadrilateral such that AB‾=2i^−3j^+k^\overline{AB}=2\widehat{i}-3\widehat{j}+\widehat{k} , BC‾=i^+j^+k^\overline{BC}=\widehat{i}+\widehat{j}+\widehat{k} , CD‾=4i^−7j^\overline{CD}=4\widehat{i}-7\widehat{j} . Then find AD‾\overline{AD} .

Explanation

Solution

Hint : As ABCD is a quadrilateral, we can use the rule of vector addition of a polygon to solve the above question. According to the rule the sum of the vectors forming all the sides of the polygon such that the tail of one vector coincides with the head of the other vector is zero. Also, use the identity that DA‾=−AD‾\overline{DA}=-\overline{AD} .

Complete step-by-step answer :
Let us start the solution to the above question by drawing a representative diagram of the situation given in the question.

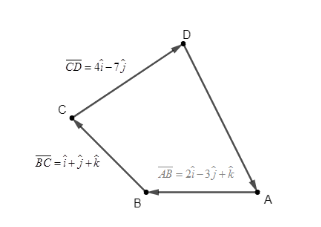
We know that according to the polygon law of vector addition the sum of the vectors forming all the sides of the polygon such that the tail of one vector coincides with the head of the other vector is zero. So, if we apply this on quadrilateral ABCD, we get
AB‾+BC‾+CD‾+DA‾=0\overline{AB}+\overline{BC}+\overline{CD}+\overline{DA}=0
Now it is given that AB‾=2i^−3j^+k^\overline{AB}=2\widehat{i}-3\widehat{j}+\widehat{k} , BC‾=i^+j^+k^\overline{BC}=\widehat{i}+\widehat{j}+\widehat{k} , CD‾=4i^−7j^\overline{CD}=4\widehat{i}-7\widehat{j} . So, if we put this values in the above equation, we get
2i^−3j^+k^+i^+j^+k^+4i^−7j^+DA‾=02\widehat{i}-3\widehat{j}+\widehat{k}+\widehat{i}+\widehat{j}+\widehat{k}+4\widehat{i}-7\widehat{j}+\overline{DA}=0
We also know that DA‾=−AD‾\overline{DA}=-\overline{AD} .
2i^−3j^+k^+i^+j^+k^+4i^−7j^−AD‾=02\widehat{i}-3\widehat{j}+\widehat{k}+\widehat{i}+\widehat{j}+\widehat{k}+4\widehat{i}-7\widehat{j}-\overline{AD}=0
⇒7i^−9j^+2k^=AD‾\Rightarrow 7\widehat{i}-9\widehat{j}+2\widehat{k}=\overline{AD}
Hence, the answer to the above question is AD‾=7i^−9j^+2k^\overline{AD}=7\widehat{i}-9\widehat{j}+2\widehat{k} .

Note : While adding the vectors, remember that the coefficients of i^,j^ and k^\widehat{i},\widehat{j}\text{ and }\widehat{k} are added separately and reported. Also, you should know that polygon law is an extension of triangle law of vector addition and the above question could have been solved using triangle law as well, but that would have been a bit lengthier. Also, remember that for applying the polygon law, the head of one vector must coincide with the tail of the other and directions of vectors are very important.