Question
Mathematics Question on circle
If ABCD is a cyclic quadrilateral with AB=6,BC=4,CD=5,DA=3 and ∠ABC = θ then cosθ =
A
133
B
7618
C
7816
D
8678
Answer
133
Explanation
Solution
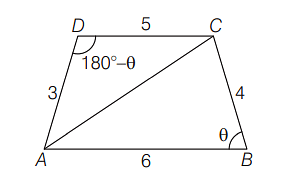
In ΔABC,
AC2=AB2+BC2−2(AB)(AC)cosθ[ By Cosine rule ]
⇒AC2=62+42−2(6)(4)cosθ
⇒AC2=36+16−48cosθ
⇒AC2=52−48cosθ…(i)
Now, In ΔADC
AC2=AD2+DC2−2(AD)(DC)cos(180∘−θ)
=32+52+2(3)(5)cosθ[ By Cosine rule ]
AC2=9+25+30cosθ
AC2=34+30cosθ…(ii)
By Eqs. (i) and (ii), we get
52−48cosθ=34+30cosθ
⇒52−34=48cosθ+30cosθ
⇒18=78cosθ
⇒cosθ=7818=133
