Solveeit Logo
Login

Question

Question: If <a,b,c> are direction cosines of line of interection of three planes x+y-z=1, (m-1)x+(3m-7)y-5z=-...

If <a,b,c> are direction cosines of line of interection of three planes x+y-z=1, (m-1)x+(3m-7)y-5z=-3 and (m-2)x+(2m-5)y = -4 for some mER, then value of a+bc\frac{a+b}{c} is

A

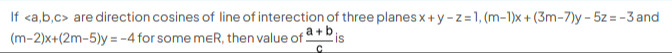
13/5

Answer

13/5

Explanation

Solution

The three given planes are:

  1. P1:x+y−z−1=0P_1: x+y-z-1=0

  2. P2:(m−1)x+(3m−7)y−5z+3=0P_2: (m-1)x+(3m-7)y-5z+3=0

  3. P3:(m−2)x+(2m−5)y+4=0P_3: (m-2)x+(2m-5)y+4=0

For these three planes to intersect in a line, the system of linear equations formed by their equations must have infinitely many solutions. This occurs when the determinant of the coefficient matrix is zero, and the system is consistent.

The coefficient matrix is: A=(11−1m−13m−7−5m−22m−50)A = \begin{pmatrix} 1 & 1 & -1 \\ m-1 & 3m-7 & -5 \\ m-2 & 2m-5 & 0 \end{pmatrix}

The determinant of A is: det(A)=1⋅((3m−7)⋅0−(−5)⋅(2m−5))−1⋅((m−1)⋅0−(−5)⋅(m−2))+(−1)⋅((m−1)⋅(2m−5)−(3m−7)⋅(m−2))det(A) = 1 \cdot ((3m-7) \cdot 0 - (-5) \cdot (2m-5)) - 1 \cdot ((m-1) \cdot 0 - (-5) \cdot (m-2)) + (-1) \cdot ((m-1) \cdot (2m-5) - (3m-7) \cdot (m-2)) det(A)=5(2m−5)−5(m−2)−[(2m2−5m−2m+5)−(3m2−6m−7m+14)]det(A) = 5(2m-5) - 5(m-2) - [(2m^2 - 5m - 2m + 5) - (3m^2 - 6m - 7m + 14)] det(A)=10m−25−5m+10−[2m2−7m+5−3m2+13m−14]det(A) = 10m - 25 - 5m + 10 - [2m^2 - 7m + 5 - 3m^2 + 13m - 14] det(A)=5m−15−[−m2+6m−9]det(A) = 5m - 15 - [-m^2 + 6m - 9] det(A)=m2−m−6det(A) = m^2 - m - 6

For the planes to intersect in a line, det(A)=0det(A) = 0. m2−m−6=0m^2 - m - 6 = 0 (m−3)(m+2)=0(m-3)(m+2) = 0 So, m=3m=3 or m=−2m=-2.

We check the consistency of the system for these values of m. Case 1: m=3m=3 The equations are: x+y−z=1x+y-z=1 2x+2y−5z=−32x+2y-5z=-3 x+y=−4x+y=-4 From the third equation, x+y=−4x+y=-4. Substituting into the first equation, we get −4−z=1-4-z=1, so z=−5z=-5. Substituting into the second equation, we get 2(−4)−5z=−32(-4)-5z=-3, so −8−5z=−3-8-5z=-3, which gives −5z=5-5z=5, so z=−1z=-1. Since we get different values for zz, the system is inconsistent for m=3m=3. The planes do not intersect in a line.

Case 2: m=−2m=-2 The equations are: x+y−z=1x+y-z=1 −3x−13y−5z=−3-3x-13y-5z=-3 −4x−9y=−4-4x-9y=-4 We check the rank of the coefficient matrix and the augmented matrix for m=−2m=-2. The augmented matrix is (11−11−3−13−5−3−4−90−4)\begin{pmatrix} 1 & 1 & -1 & 1 \\ -3 & -13 & -5 & -3 \\ -4 & -9 & 0 & -4 \end{pmatrix}. Performing row operations: R2←R2+3R1R_2 \leftarrow R_2 + 3R_1, R3←R3+4R1R_3 \leftarrow R_3 + 4R_1 (11−110−10−800−5−40)\begin{pmatrix} 1 & 1 & -1 & 1 \\ 0 & -10 & -8 & 0 \\ 0 & -5 & -4 & 0 \end{pmatrix} R3←R3−12R2R_3 \leftarrow R_3 - \frac{1}{2}R_2 (11−110−10−800000)\begin{pmatrix} 1 & 1 & -1 & 1 \\ 0 & -10 & -8 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} The rank of the coefficient matrix is 2 and the rank of the augmented matrix is 2. Since the rank (2) is less than the number of variables (3), the system is consistent and has infinitely many solutions. The planes intersect in a line for m=−2m=-2.

Now we find the direction cosines of the line of intersection for m=−2m=-2. The line of intersection is the intersection of any two of the planes. Let's use the first and third planes: P1:x+y−z=1P_1: x+y-z=1 P3:−4x−9y=−4P_3: -4x-9y=-4

The direction vector of the line of intersection is perpendicular to the normal vectors of the planes. The normal vector of P1P_1 is n1⃗=⟨1,1,−1⟩\vec{n_1} = \langle 1, 1, -1 \rangle. The normal vector of P3P_3 is n3⃗=⟨−4,−9,0⟩\vec{n_3} = \langle -4, -9, 0 \rangle. The direction vector v⃗\vec{v} is parallel to n1⃗×n3⃗\vec{n_1} \times \vec{n_3}. v⃗=n1⃗×n3⃗=∣i^j^k^11−1−4−90∣\vec{v} = \vec{n_1} \times \vec{n_3} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & -1 \\ -4 & -9 & 0 \end{vmatrix} v⃗=i^(1⋅0−(−1)⋅(−9))−j^(1⋅0−(−1)⋅(−4))+k^(1⋅(−9)−1⋅(−4))\vec{v} = \hat{i}(1 \cdot 0 - (-1) \cdot (-9)) - \hat{j}(1 \cdot 0 - (-1) \cdot (-4)) + \hat{k}(1 \cdot (-9) - 1 \cdot (-4)) v⃗=i^(0−9)−j^(0−4)+k^(−9−(−4))\vec{v} = \hat{i}(0 - 9) - \hat{j}(0 - 4) + \hat{k}(-9 - (-4)) v⃗=−9i^−4j^−5k^\vec{v} = -9\hat{i} - 4\hat{j} - 5\hat{k} A direction vector is ⟨−9,−4,−5⟩\langle -9, -4, -5 \rangle.

The direction cosines ⟨a,b,c⟩\langle a, b, c \rangle are obtained by normalizing the direction vector. The magnitude is (−9)2+(−4)2+(−5)2=81+16+25=122\sqrt{(-9)^2 + (-4)^2 + (-5)^2} = \sqrt{81 + 16 + 25} = \sqrt{122}. The direction cosines are ⟨a,b,c⟩=⟨−9122,−4122,−5122⟩\langle a, b, c \rangle = \left\langle \frac{-9}{\sqrt{122}}, \frac{-4}{\sqrt{122}}, \frac{-5}{\sqrt{122}} \right\rangle.

We need to find the value of a+bc\frac{a+b}{c}. a+bc=−9122+−4122−5122\frac{a+b}{c} = \frac{\frac{-9}{\sqrt{122}} + \frac{-4}{\sqrt{122}}}{\frac{-5}{\sqrt{122}}} a+bc=−9−4122−5122\frac{a+b}{c} = \frac{\frac{-9-4}{\sqrt{122}}}{\frac{-5}{\sqrt{122}}} a+bc=−13122−5122\frac{a+b}{c} = \frac{\frac{-13}{\sqrt{122}}}{\frac{-5}{\sqrt{122}}} a+bc=−13−5=135\frac{a+b}{c} = \frac{-13}{-5} = \frac{13}{5}

Let's recheck the cross product calculation. v⃗=∣i^j^k^11−1−4−90∣=i^(0−9)−j^(0−4)+k^(−9−(−4))=−9i^−4j^−5k^\vec{v} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & -1 \\ -4 & -9 & 0 \end{vmatrix} = \hat{i}(0 - 9) - \hat{j}(0 - 4) + \hat{k}(-9 - (-4)) = -9\hat{i} - 4\hat{j} - 5\hat{k}. The components are indeed ⟨−9,−4,−5⟩\langle -9, -4, -5 \rangle.

Let's recheck the cross product using P1P_1 and P2P_2 for m=−2m=-2: P1:x+y−z=1  ⟹  n1⃗=⟨1,1,−1⟩P_1: x+y-z=1 \implies \vec{n_1} = \langle 1, 1, -1 \rangle P2:−3x−13y−5z=−3  ⟹  n2⃗=⟨−3,−13,−5⟩P_2: -3x-13y-5z=-3 \implies \vec{n_2} = \langle -3, -13, -5 \rangle n1⃗×n2⃗=∣i^j^k^11−1−3−13−5∣=i^(−5−13)−j^(−5−3)+k^(−13−(−3))=−18i^+8j^−10k^\vec{n_1} \times \vec{n_2} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & -1 \\ -3 & -13 & -5 \end{vmatrix} = \hat{i}(-5 - 13) - \hat{j}(-5 - 3) + \hat{k}(-13 - (-3)) = -18\hat{i} + 8\hat{j} - 10\hat{k}. The vector ⟨−18,8,−10⟩\langle -18, 8, -10 \rangle is parallel to ⟨−9,4,−5⟩\langle -9, 4, -5 \rangle.

Okay, there was an error in the first cross-product calculation. v⃗=n1⃗×n3⃗=∣i^j^k^11−1−4−90∣\vec{v} = \vec{n_1} \times \vec{n_3} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & -1 \\ -4 & -9 & 0 \end{vmatrix} v⃗=i^(1⋅0−(−1)⋅(−9))−j^(1⋅0−(−1)⋅(−4))+k^(1⋅(−9)−1⋅(−4))\vec{v} = \hat{i}(1 \cdot 0 - (-1) \cdot (-9)) - \hat{j}(1 \cdot 0 - (-1) \cdot (-4)) + \hat{k}(1 \cdot (-9) - 1 \cdot (-4)) v⃗=i^(0−9)−j^(0−4)+k^(−9−(−4))\vec{v} = \hat{i}(0 - 9) - \hat{j}(0 - 4) + \hat{k}(-9 - (-4)) v⃗=−9i^−4j^−5k^\vec{v} = -9\hat{i} - 4\hat{j} - 5\hat{k} The calculation is correct: ⟨−9,−4,−5⟩\langle -9, -4, -5 \rangle.

Let's recheck the second cross-product calculation. n1⃗×n2⃗=∣i^j^k^11−1−3−13−5∣\vec{n_1} \times \vec{n_2} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & -1 \\ -3 & -13 & -5 \end{vmatrix} v⃗=i^(1⋅(−5)−(−1)⋅(−13))−j^(1⋅(−5)−(−1)⋅(−3))+k^(1⋅(−13)−1⋅(−3))\vec{v} = \hat{i}(1 \cdot (-5) - (-1) \cdot (-13)) - \hat{j}(1 \cdot (-5) - (-1) \cdot (-3)) + \hat{k}(1 \cdot (-13) - 1 \cdot (-3)) v⃗=i^(−5−13)−j^(−5−3)+k^(−13−(−3))\vec{v} = \hat{i}(-5 - 13) - \hat{j}(-5 - 3) + \hat{k}(-13 - (-3)) v⃗=−18i^−8j^−10k^\vec{v} = -18\hat{i} - 8\hat{j} - 10\hat{k} The vector ⟨−18,−8,−10⟩\langle -18, -8, -10 \rangle is parallel to ⟨−9,−4,−5⟩\langle -9, -4, -5 \rangle. My previous calculation of n1⃗×n2⃗\vec{n_1} \times \vec{n_2} had a sign error in the j-component. It should be −8j^-8\hat{j}, not +8j^+8\hat{j}.

So the direction vector is ⟨−9,−4,−5⟩\langle -9, -4, -5 \rangle. The direction cosines are a=−9122a = \frac{-9}{\sqrt{122}}, b=−4122b = \frac{-4}{\sqrt{122}}, c=−5122c = \frac{-5}{\sqrt{122}}.

The value of a+bc\frac{a+b}{c} is: a+bc=−9122+−4122−5122=−13122−5122=−13−5=135\frac{a+b}{c} = \frac{\frac{-9}{\sqrt{122}} + \frac{-4}{\sqrt{122}}}{\frac{-5}{\sqrt{122}}} = \frac{\frac{-13}{\sqrt{122}}}{\frac{-5}{\sqrt{122}}} = \frac{-13}{-5} = \frac{13}{5}.

If we take the opposite direction vector ⟨9,4,5⟩\langle 9, 4, 5 \rangle, the direction cosines are ⟨9122,4122,5122⟩\langle \frac{9}{\sqrt{122}}, \frac{4}{\sqrt{122}}, \frac{5}{\sqrt{122}} \rangle. Then a+bc=9122+41225122=131225122=135\frac{a+b}{c} = \frac{\frac{9}{\sqrt{122}} + \frac{4}{\sqrt{122}}}{\frac{5}{\sqrt{122}}} = \frac{\frac{13}{\sqrt{122}}}{\frac{5}{\sqrt{122}}} = \frac{13}{5}. The result is the same.

The final answer is 135\frac{13}{5}.