Solveeit Logo
Login

Question

Question: If AB is a double ordinate of the hyperbola \(\dfrac{{{{\text{x}}^2}}}{{{{\text{a}}^2}}} - \dfrac{{{...

If AB is a double ordinate of the hyperbola x2a2−y2b2=1\dfrac{{{{\text{x}}^2}}}{{{{\text{a}}^2}}} - \dfrac{{{{\text{y}}^2}}}{{{{\text{b}}^2}}} = 1 such that ∆AOB (O is the origin) is an equilateral triangle, then the eccentricity e of the hyperbola satisfies:
A. e > 3 B. 1 < e < 23 C. e = 23 D. e > 23  {\text{A}}{\text{. e > }}\sqrt 3 \\\ {\text{B}}{\text{. 1 < e < }}\dfrac{2}{{\sqrt 3 }} \\\ {\text{C}}{\text{. e = }}\dfrac{2}{{\sqrt 3 }} \\\ {\text{D}}{\text{. e > }}\dfrac{2}{{\sqrt 3 }} \\\

Explanation

Solution

Hint: According to the given data in the question, we draw an appropriate figure that helps us find the coordinates of points A and B. Also given AOB is an equilateral triangle, i.e. all angles in the triangle are equal to 60°.

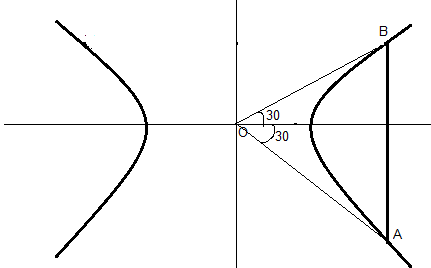
Complete step-by-step answer:

Given O (0, 0) is the origin and AB is the double ordinate of the hyperbola i.e. polar coordinates of
A = (a secθ, b tanθ), B = (a secθ, -b tanθ).
Since ∆AOB is equilateral, OA = AB
We use the formula for distance between two points (d2^2 =(x2−x1)2+(y2−y1)2{\left( {{{\text{x}}_2} - {{\text{x}}_1}} \right)^2} + {\left( {{{\text{y}}_2} - {{\text{y}}_1}} \right)^2}), to form a relation OA = AB, which give us
(asecθ - 0)2+(-btan⁡θ−0)2=(asecθ - asecθ)2+(btanθ - (−btanθ))2\sqrt {{{\left( {{\text{asec}}\theta {\text{ - 0}}} \right)}^2} + {{\left( {{\text{-b}}\tan \theta - 0} \right)}^2}} = \sqrt {{{\left( {{\text{asec}}\theta {\text{ - asec}}\theta } \right)}^2} + {{\left( {{\text{btan}}\theta {\text{ - }}\left( { - {\text{btan}}\theta } \right)} \right)}^2}}
⇒a2sec2θ+b2tan2θ=4b2tan⁡2θ\Rightarrow {{\text{a}}^2}{\text{se}}{{\text{c}}^2}\theta + {{\text{b}}^2}{\text{ta}}{{\text{n}}^2}\theta = 4{{\text{b}}^2}{\tan ^2}\theta
⇒a2sec2θ=3b2tan⁡2θ\Rightarrow {{\text{a}}^2}{\text{se}}{{\text{c}}^2}\theta = 3{{\text{b}}^2}{\tan ^2}\theta -- (1)
We know according to trigonometric identities, sec2θ−tan2θ= 1{\text{se}}{{\text{c}}^2}\theta - {\text{ta}}{{\text{n}}^2}\theta = {\text{ 1}}
Hencesec2θ=1+tan2θ{\text{se}}{{\text{c}}^2}\theta = 1 + {\text{ta}}{{\text{n}}^2}\theta , substitute this in equation (1), we get
a2+a2tan2θ=3b2tan2θ{{\text{a}}^2} + {{\text{a}}^2}{\text{ta}}{{\text{n}}^2}\theta = 3{{\text{b}}^2}{\text{ta}}{{\text{n}}^2}\theta
⇒b2a2=1+tan2θ3tan2θ\Rightarrow \dfrac{{{{\text{b}}^2}}}{{{{\text{a}}^2}}} = \dfrac{{1 + {\text{ta}}{{\text{n}}^2}\theta }}{{3{\text{ta}}{{\text{n}}^2}\theta }}
Now we know for eccentricity e2=1+b2a2{{\text{e}}^2} = 1 + \dfrac{{{{\text{b}}^2}}}{{{{\text{a}}^2}}}=1+1+tan2θ3tan2θ1 + \dfrac{{1 + {\text{ta}}{{\text{n}}^2}\theta }}{{3{\text{ta}}{{\text{n}}^2}\theta }}=1+4tan2θ3tan2θ\dfrac{{1 + 4{\text{ta}}{{\text{n}}^2}\theta }}{{3{\text{ta}}{{\text{n}}^2}\theta }}
= 43\dfrac{4}{3} +13sin2θ\dfrac{1}{{3{\text{si}}{{\text{n}}^2}\theta }}.
Usingsin2θ < 1{\text{si}}{{\text{n}}^2}\theta {\text{ < 1}}, we get e2 > 43{{\text{e}}^2}{\text{ > }}\dfrac{4}{3}
Hence e >23\dfrac{2}{{\sqrt 3 }}. Option D is the correct answer.

Note: In order to solve these types of questions the key concept is to carefully draw a precise figure according to the given data. Then we use the figure to derive necessary relations which help us compute the solution. Basic knowledge of geometrical formulae of hyperbola, its eccentricity and trigonometric functions is very important in solving these problems.