Solveeit Logo
Login

Question

Question: If AB is a double ordinate of the hyperbola \[\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2...

If AB is a double ordinate of the hyperbola x2a2−y2b2=1\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 such that △OAB is an equilateral triangle, O being the origin, then the eccentricity of the hyperbola satisfies:
A. e>3e >\sqrt{3}
B. 1<e<231< e <\dfrac{2}{\sqrt{3}}
C. e=23e=\dfrac{2}{\sqrt{3}}
D. e>23e>\dfrac{2}{\sqrt{3}}

Explanation

Solution

Hint: First we have to consider the double ordinate length. From that we will get the ordinate. By using this we have to find the abscissa. From that we have to do a set of operations to find the value of e.

Complete step-by-step solution -
__
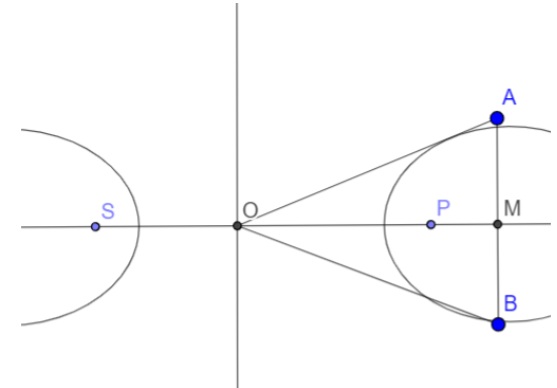
Let the length of the double ordinate be 2l2l.
From the figure AB = 2l2l, AM = ll, BM= ll.
The ordinate of point A is l.
We have to find the abscissa of the point A, that is by substituting the value of ordinate in the hyperbola equation.
x2a2−l2b2=1\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{l}^{2}}}{{{b}^{2}}}=1
x2a2=1+l2b2\dfrac{{{x}^{2}}}{{{a}^{2}}}=1+\dfrac{{{l}^{2}}}{{{b}^{2}}}
x2=a2(1+l2b2){{x}^{2}}={{a}^{2}}\left( 1+\dfrac{{{l}^{2}}}{{{b}^{2}}} \right)
x=a(b2+l2)bx=\dfrac{a\left( \sqrt{{{b}^{2}}+{{l}^{2}}} \right)}{b} . . . . . . . . . . . . . . . . . . . . . . . (1)
Therefore point A is (a(b2+l2)b,l)\left( \dfrac{a\left( \sqrt{{{b}^{2}}+{{l}^{2}}} \right)}{b},l \right)
Given that △OAB is an equilateral triangle, therefore
OA=OB=AB=2lOA=OB=AB=2l
From Pythagoras theorem, we get OM2+AM2=OA2O{{M}^{2}}+A{{M}^{2}}=O{{A}^{2}}
⇒a2(b2+l2)b2+l2=4l2\Rightarrow \dfrac{{{a}^{2}}\left( {{b}^{2}}+{{l}^{2}} \right)}{{{b}^{2}}}+{{l}^{2}}=4{{l}^{2}}
⇒l2=a2b23b2−a2\Rightarrow {{l}^{2}}=\dfrac{{{a}^{2}}{{b}^{2}}}{3{{b}^{2}}-{{a}^{2}}}
Here l2>0{{l}^{2}}>0
⇒a2b23b2−a2>0\Rightarrow \dfrac{{{a}^{2}}{{b}^{2}}}{3{{b}^{2}}-{{a}^{2}}}>0 . . . . . . . . . . . . . . . . . . . . . . (2)
⇒3b2−a2>0\Rightarrow 3{{b}^{2}}-{{a}^{2}}>0
Now, e2=1+b2a2{{e}^{2}}=1+\dfrac{{{b}^{2}}}{{{a}^{2}}} . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . (a)
Writing in terms of
b2=a2(e2−1){{b}^{2}}={{a}^{2}}\left( {{e}^{2}}-1 \right)
⇒3a2(e2−1)−a2>0\Rightarrow 3{{a}^{2}}\left( {{e}^{2}}-1 \right)-{{a}^{2}}>0
By further solving,
e2>13+1{{e}^{2}}>\dfrac{1}{3}+1
⇒e2>43\Rightarrow {{e}^{2}}>\dfrac{4}{3}
⇒e>23\Rightarrow e > \dfrac{2}{\sqrt{3}}
Therefore the answer is option D.

Note: The term (a) is the eccentricity. In (2) we have taken only 3b2−a23{{b}^{2}}-{{a}^{2}} because in the numerator a2b2{{a}^{2}}{{b}^{2}} is there which is a positive term for the ll to become >0 the denominator term should not be negative. So we have taken that term in the denominator.