Solveeit Logo
Login

Question

Question: If AB=d and \[{{d}_{1}},\text{ }{{d}_{2}}~\text{and }{{d}_{3}}\] are the projections of the line seg...

If AB=d and d1, d2 and d3{{d}_{1}},\text{ }{{d}_{2}}~\text{and }{{d}_{3}} are the projections of the line segment AB on the coordinate planes, then d2={{d}^{2}}=
a) d12+d22+d322\dfrac{d_{1}^{2}+d_{2}^{2}+d_{3}^{2}}{2}
b) d1+d2+d33\dfrac{{{d}_{1}}+{{d}_{2}}+{{d}_{3}}}{3}
c) d1d2d32\dfrac{{{d}_{1}}{{d}_{2}}{{d}_{3}}}{2}
d) 2(d12+d22+d32)2\left( d_{1}^{2}+d_{2}^{2}+d_{3}^{2} \right)

Explanation

Solution

Hint : In this question, we are given a line segment AB and are asked to find the relation between its length and the lengths of its projections on the coordinate planes. As in a projection on a coordinate plane the coordinates corresponding to the coordinate axes not belonging to the plane should be set to zero and those coordinates belonging to the plane should remain unchanged, we can assume the coordinates of A and B to be (xA,yA,zA)\left( {{x}_{A}},{{y}_{A}},{{z}_{A}} \right) and (xB,yB,zB)\left( {{x}_{B}},{{y}_{B}},{{z}_{B}} \right) respectively, find the coordinates of the projections and use the distance formula to find the length of the projections and hence the required relation which is asked in the question.

Complete step by step solution :
Let AB be be line segment such that the coordinates of A and B are (xA,yA,zA)\left( {{x}_{A}},{{y}_{A}},{{z}_{A}} \right) and (xB,yB,zB)\left( {{x}_{B}},{{y}_{B}},{{z}_{B}} \right) respectively.

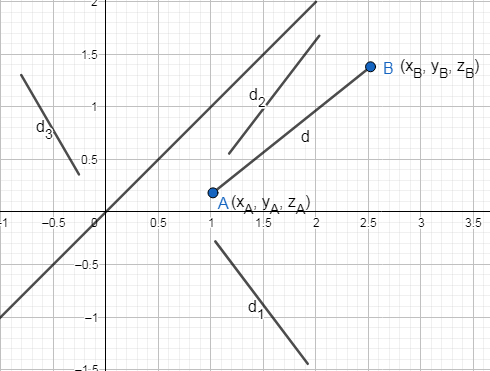
Now, we know that the square of the distance(r) between two points (x1,y1,z1)\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) and (x2,y2,z2)\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) is given by
r2=(x1−x2)2+(y1−y2)2+(z1−z2)2{{r}^{2}}={{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}+{{\left( {{z}_{1}}-{{z}_{2}} \right)}^{2}} ………………………………………(1.1)
Therefore, as the length of AB is the distance between the points A and B and it given to be d, we can write
d2=(xA−xB)2+(yA−yB)2+(zA−zB)2{{d}^{2}}={{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+{{\left( {{y}_{A}}-{{y}_{B}} \right)}^{2}}+{{\left( {{z}_{A}}-{{z}_{B}} \right)}^{2}} ……………………………..(1.2)
Also, we know that in a projection on a coordinate plane the coordinates corresponding to the coordinate axes not belonging to the plane should be set to zero and those coordinates belonging to the plane should remain unchanged.
Therefore, upon projection onto the x-y plane, the x and y coordinates of A and B should remain unchanged and the z coordinates should be set to zero, therefore, using (1.1) and (1.2), the length of the projection of AB onto the x-y plane should be given by
d12=(xA−xB)2+(yA−yB)2+(0−0)2=(xA−xB)2+(yA−yB)2{{d}_{1}}^{2}={{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+{{\left( {{y}_{A}}-{{y}_{B}} \right)}^{2}}+{{\left( 0-0 \right)}^{2}}={{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+{{\left( {{y}_{A}}-{{y}_{B}} \right)}^{2}} ………………………………(1.3)
Similarly, upon projection onto the y-z plane, the y and z coordinates of A and B should remain unchanged and the x coordinates should be set to zero, therefore, using (1.1) and (1.2), the length of the projection of AB onto the x-y plane should be given by
d22=(0−0)2+(yA−yB)2+(zA−zB)2=(yA−yB)2+(zA−zB)2{{d}_{2}}^{2}={{\left( 0-0 \right)}^{2}}+{{\left( {{y}_{A}}-{{y}_{B}} \right)}^{2}}+{{\left( {{z}_{A}}-{{z}_{B}} \right)}^{2}}={{\left( {{y}_{A}}-{{y}_{B}} \right)}^{2}}+{{\left( {{z}_{A}}-{{z}_{B}} \right)}^{2}} ………………………………(1.4)
Upon projection onto the x-z plane, the x and z coordinates of A and B should remain unchanged and the y coordinates should be set to zero, therefore, using (1.1) and (1.2), the length of the projection of AB onto the x-y plane should be given by
d32=(xA−xB)2+(0−0)2+(zA−zB)2=(xA−xB)2+(zA−zB)2{{d}_{3}}^{2}={{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+{{\left( 0-0 \right)}^{2}}+{{\left( {{z}_{A}}-{{z}_{B}} \right)}^{2}}={{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+{{\left( {{z}_{A}}-{{z}_{B}} \right)}^{2}} ………………………………(1.5)
Adding (1.3), (1.4) and (1.5), and using (1.2), we obtain

& d_{1}^{2}+d_{2}^{2}+d_{3}^{2}=2{{\left( {{x}_{A}}-{{x}_{B}} \right)}^{2}}+2{{\left( {{y}_{A}}-{{y}_{B}} \right)}^{2}}+2{{\left( {{z}_{A}}-{{z}_{B}} \right)}^{2}}=2{{d}^{2}} \\\ & \Rightarrow {{d}^{2}}=\dfrac{d_{1}^{2}+d_{2}^{2}+d_{3}^{2}}{2} \\\ \end{aligned}$$ Which matches option(a) of the question. Therefore, option (a) is the correct answer to this question. **Note** : We should note that we have taken ${{d}_{1}}$ as the projection of AB onto the x-y plane, ${{d}_{2}}$ as the projection of AB onto the y-z plane and ${{d}_{3}}$ as the projection of AB onto the x-z plane. However, one can interchange the names ${{d}_{1}},{{d}_{2}}\text{ and }{{d}_{3}}$ for the projections as ultimately we would be adding all the squares of the three projections and thus the particular order of naming will not affect the solution.