Question
Question: If A+B = $\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}$ and A-2B = $\begin{bmatrix} -1 & 1 \\ 0 & -1...
If A+B = [1111] and A-2B = [−101−1], then A
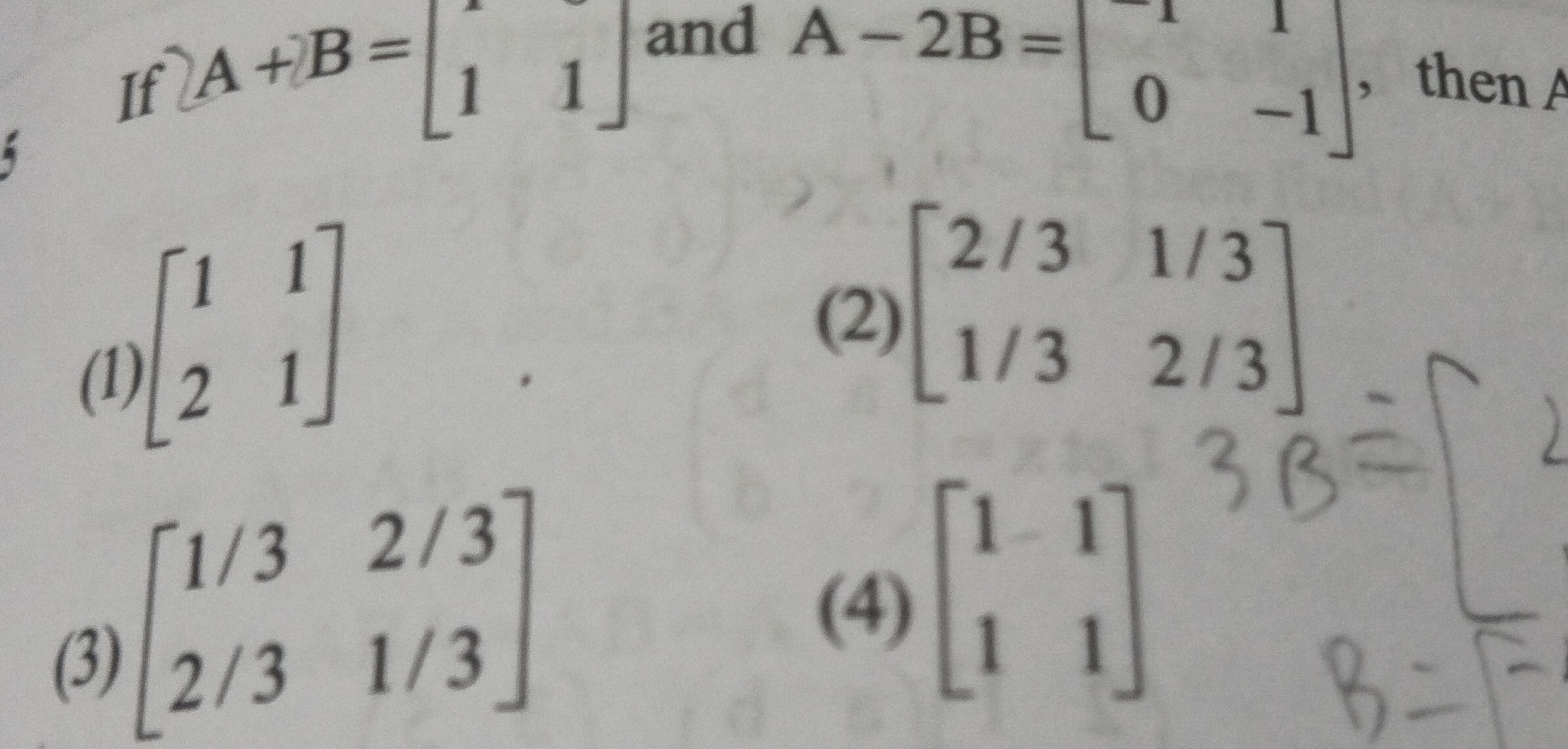
[1211]
[2/31/31/32/3]
[1/32/32/31/3]
[1111]
[1/32/311/3]
Solution
Let the given equations be:
-
A+B=[1111]
-
A−2B=[−101−1]
We have a system of two linear equations with two matrix variables, A and B. We can solve this system using methods similar to solving algebraic equations.
Multiply equation (1) by 2:
2(A+B)=2[1111]
2A+2B=[2222] (Equation 3)
Now, add equation (3) and equation (2):
(2A+2B)+(A−2B)=[2222]+[−101−1]
Combine the terms involving A and B on the left side:
(2A+A)+(2B−2B)=3A+0=3A
Add the matrices on the right side:
[2222]+[−101−1]=[2+(−1)2+02+12+(−1)]=[1231]
So, we have:
3A=[1231]
To find A, multiply the matrix by the scalar 31:
A=31[1231]
A=[31×131×231×331×1]
A=[1/32/311/3]
The calculated matrix A is [1/32/311/3]. This does not match any of the provided options. There appears to be an error in the provided options.
