Question
Question: If $A+B = \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix}$ and $A-2B = \begin{bmatrix} -1 & 1 \\ 0 & -1...
If A+B=[1101] and A−2B=[−101−1], then A
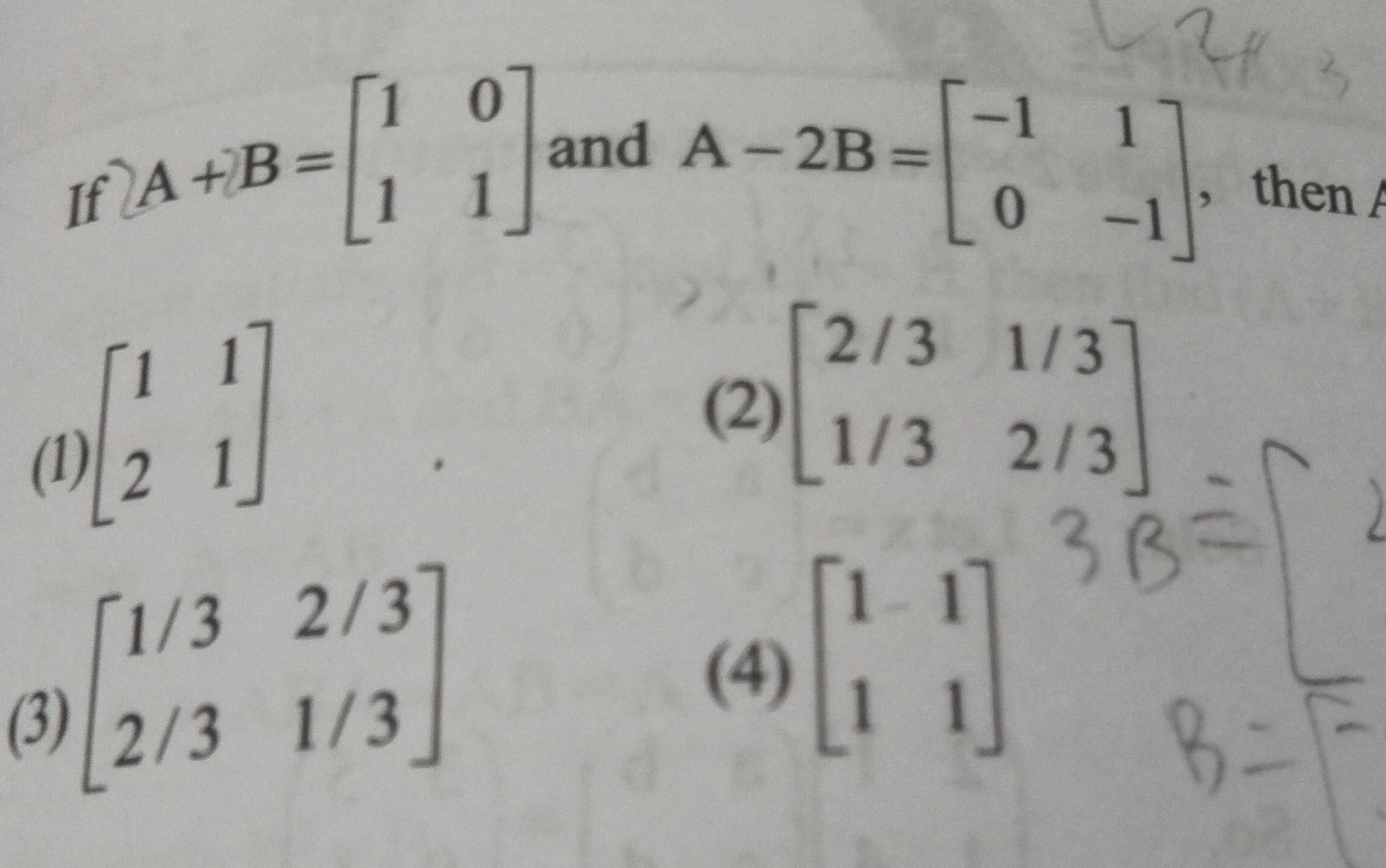
A
[1211]
B
[2/31/31/32/3]
C
[1/32/32/31/3]
D
[11−11]
Answer
[1/32/31/31/3]
Explanation
Solution
We are given the following matrix equations:
-
A+B=[1101]
-
A−2B=[−101−1]
We can solve this system of equations for the matrix A. Multiply the first equation by 2:
2(A+B)=2[1101]
2A+2B=[2202] (Equation 3)
Now, add Equation 2 and Equation 3:
(A−2B)+(2A+2B)=[−101−1]+[2202]
(A+2A)+(−2B+2B)=[−1+20+21+0−1+2]
3A+0=[1211]
3A=[1211]
To find A, multiply the matrix by the scalar 31:
A=31[1211]
A=[31×131×231×131×1]
A=[1/32/31/31/3]
Comparing this result with the given options, we find that none of the options exactly match the calculated matrix A.
