Question

If $AB$ and $CD$ are two chords of a circle which when produced to meet at a point $P$ such that $AB = 5{\rm{cm}}$, $AP = 8{\rm{cm}}$ and $CD = 2{\rm{cm}}$ then $PD =$
A.12 cm
B.5 cm
C.6 cm
D.cm

Answer 1

Here, we will first draw a figure using the given information. Then we will use the intersecting secant theorem to frame a quadratic equation. We will then solve the obtained equation by factorization method to the required length of $PD$.

Complete step-by-step answer:
According to the question,
$AB$and $CD$ are two chords of a circle
Also, they are produced to meet at a point $P$.
It is given that $AB = 5{\rm{cm}}$, $AP = 8{\rm{cm}}$and $CD = 2{\rm{cm}}$
And, we are required to find the length of $PD$

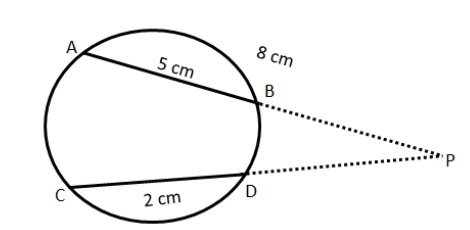
Now, by intersecting secant theorem, we know that,
$PA \times PB = PC \times PD$……………………………………$\left( 1 \right)$
Now from the figure we can see, $PC = \left( {PD + CD} \right)$
And, it is given that $AP = 8{\rm{cm}}$
Also, $AB = 5{\rm{cm}}$ and $AP = 8{\rm{cm}}$,
Therefore, $PB = \left( {AP - AB} \right) = \left( {8 - 5} \right) = 3{\rm{cm}}$
Hence, substituting these values in equation $\left( 1 \right)$, we get,
$8 \times 3 = \left( {PD + CD} \right) \times PD$
According to the question, $CD = 2{\rm{cm}}$, hence substituting this value,
$\Rightarrow 24 = \left( {PD + 2} \right) \times PD$
Now, opening the brackets and solving further, we get,
$\Rightarrow P{D^2} + 2PD - 24 = 0$
The above equation is a quadratic equation. We will factorize this equation to find the required value.
Splitting the middle term, we get
$\Rightarrow P{D^2} + 6PD - 4PD - 24 = 0$
$\Rightarrow PD\left( PD+6 \right)-4\left( PD+6 \right)=0$
Taking the brackets common, we get
$\Rightarrow \left( {PD - 4} \right)\left( {PD + 6} \right) = 0$
By zero product property, we get
$\Rightarrow \left( {PD - 4} \right) = 0$
$\Rightarrow PD = 4{\rm{cm}}$
Or
$\Rightarrow \left( {PD + 6} \right) = 0$
$\Rightarrow PD = - 6{\rm{cm}}$
But, length can’ be negative.
Therefore, rejecting the negative value, we get,
$PD = 4{\rm{cm}}$
Hence, option D is the correct answer.

Note: A chord of a circle is a straight line segment whose endpoints lie on the circumference of the circle. By intersecting secant theorem, we mean that if two secant segments are drawn to a circle from an external point then the product of one internal and external secant is equal to the product of the second internal and external secant. Here, secant is a straight line that cuts a circle at two or more parts.