Solveeit Logo
Login

Question

Question: If $a_k = 1 + cos(\frac{k\pi}{20}) + sin(\frac{k\pi}{20})$, $\frac{1}{2} - sin(\frac{k\pi}{10})$, $k...

If ak=1+cos(kπ20)+sin(kπ20)a_k = 1 + cos(\frac{k\pi}{20}) + sin(\frac{k\pi}{20}), 12−sin(kπ10)\frac{1}{2} - sin(\frac{k\pi}{10}), k∈Nk \in N then-

यदि ak=1+cos(kπ20)+sin(kπ20)a_k = 1 + cos(\frac{k\pi}{20}) + sin(\frac{k\pi}{20}), 12−sin(kπ10)\frac{1}{2} - sin(\frac{k\pi}{10}), k∈Nk \in N तब-

A

a1+a3=a21+a23a_1 + a_3 = a_{21} + a_{23}

B

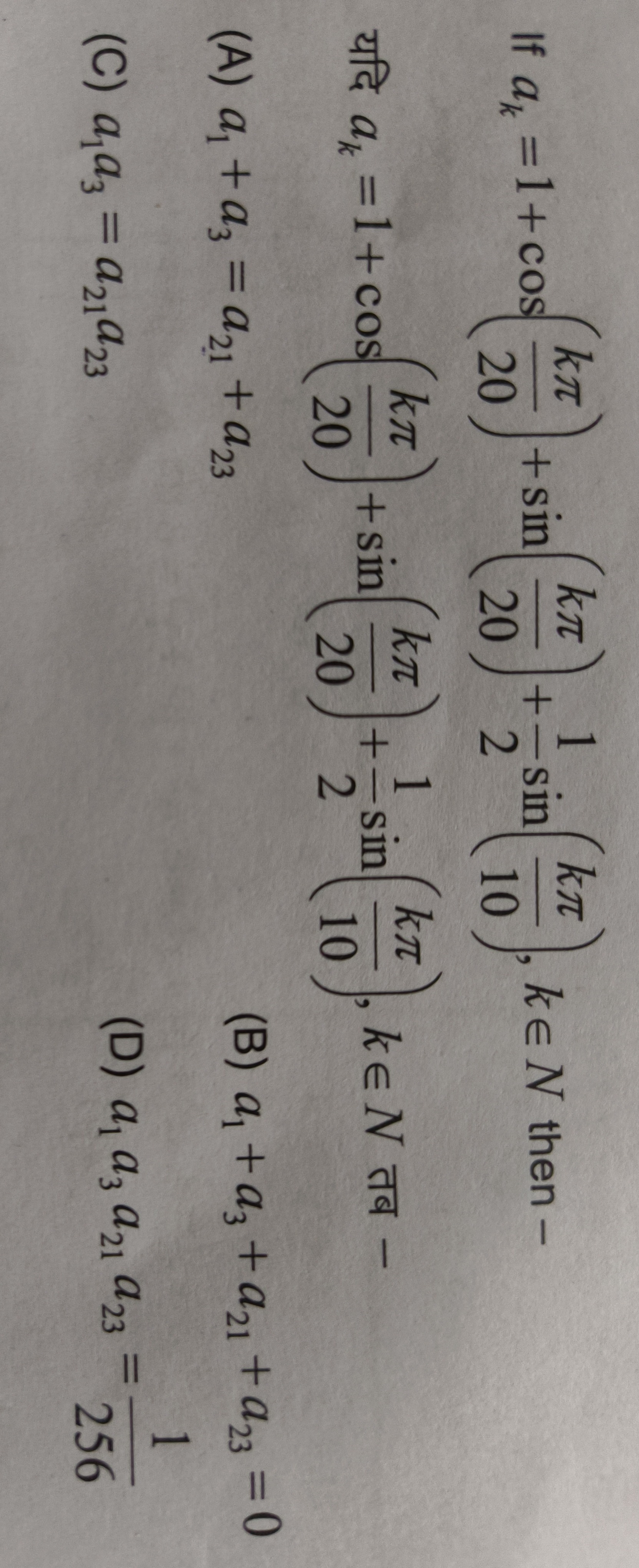
a1+a3+a21+a23=0a_1 + a_3 + a_{21} + a_{23} = 0

C

a1a3=a21a23a_1 a_3 = a_{21} a_{23}

D

a1a3a21a23=1256a_1 a_3 a_{21} a_{23} = \frac{1}{256}

Answer

None of the options are correct

Explanation

Solution

Let ak=(1+cos⁡(kπ20)+sin⁡(kπ20))(12−sin⁡(kπ10))a_k = \left(1 + \cos\left(\frac{k\pi}{20}\right) + \sin\left(\frac{k\pi}{20}\right)\right) \left(\frac{1}{2} - \sin\left(\frac{k\pi}{10}\right)\right).
Let Pk=1+cos⁡(kπ20)+sin⁡(kπ20)P_k = 1 + \cos\left(\frac{k\pi}{20}\right) + \sin\left(\frac{k\pi}{20}\right) and Qk=12−sin⁡(kπ10)Q_k = \frac{1}{2} - \sin\left(\frac{k\pi}{10}\right).
We observe the following properties for k∈{1,3}k \in \{1, 3\}:

  1. Pk+20=1+cos⁡((k+20)π20)+sin⁡((k+20)π20)=1+cos⁡(kπ20+π)+sin⁡(kπ20+π)=1−cos⁡(kπ20)−sin⁡(kπ20)P_{k+20} = 1 + \cos\left(\frac{(k+20)\pi}{20}\right) + \sin\left(\frac{(k+20)\pi}{20}\right) = 1 + \cos\left(\frac{k\pi}{20} + \pi\right) + \sin\left(\frac{k\pi}{20} + \pi\right) = 1 - \cos\left(\frac{k\pi}{20}\right) - \sin\left(\frac{k\pi}{20}\right).
    Thus, Pk+Pk+20=2P_k + P_{k+20} = 2.
    And PkPk+20=(1+(cos⁡(kπ20)+sin⁡(kπ20)))(1−(cos⁡(kπ20)+sin⁡(kπ20)))P_k P_{k+20} = \left(1 + \left(\cos\left(\frac{k\pi}{20}\right) + \sin\left(\frac{k\pi}{20}\right)\right)\right) \left(1 - \left(\cos\left(\frac{k\pi}{20}\right) + \sin\left(\frac{k\pi}{20}\right)\right)\right)
    =1−(cos⁡(kπ20)+sin⁡(kπ20))2=1−(cos⁡2(kπ20)+sin⁡2(kπ20)+2sin⁡(kπ20)cos⁡(kπ20))= 1 - \left(\cos\left(\frac{k\pi}{20}\right) + \sin\left(\frac{k\pi}{20}\right)\right)^2 = 1 - \left(\cos^2\left(\frac{k\pi}{20}\right) + \sin^2\left(\frac{k\pi}{20}\right) + 2\sin\left(\frac{k\pi}{20}\right)\cos\left(\frac{k\pi}{20}\right)\right)
    =1−(1+sin⁡(2kπ20))=1−(1+sin⁡(kπ10))=−sin⁡(kπ10)= 1 - \left(1 + \sin\left(\frac{2k\pi}{20}\right)\right) = 1 - \left(1 + \sin\left(\frac{k\pi}{10}\right)\right) = -\sin\left(\frac{k\pi}{10}\right).

  2. Qk+20=12−sin⁡((k+20)π10)=12−sin⁡(kπ10+2π)=12−sin⁡(kπ10)Q_{k+20} = \frac{1}{2} - \sin\left(\frac{(k+20)\pi}{10}\right) = \frac{1}{2} - \sin\left(\frac{k\pi}{10} + 2\pi\right) = \frac{1}{2} - \sin\left(\frac{k\pi}{10}\right).
    Thus, Qk=Qk+20Q_k = Q_{k+20}.

Now we evaluate the given options:
(A) a1+a3=a21+a23a_1 + a_3 = a_{21} + a_{23}
P1Q1+P3Q3=P21Q1+P23Q3P_1 Q_1 + P_3 Q_3 = P_{21} Q_1 + P_{23} Q_3
(P1−P21)Q1+(P3−P23)Q3=0(P_1 - P_{21})Q_1 + (P_3 - P_{23})Q_3 = 0
(2cos⁡(π20)+2sin⁡(π20))Q1+(2cos⁡(3π20)+2sin⁡(3π20))Q3=0(2\cos(\frac{\pi}{20}) + 2\sin(\frac{\pi}{20}))Q_1 + (2\cos(\frac{3\pi}{20}) + 2\sin(\frac{3\pi}{20}))Q_3 = 0.
This simplifies to (cos⁡(π20)+sin⁡(π20))Q1+(cos⁡(3π20)+sin⁡(3π20))Q3=0(\cos(\frac{\pi}{20}) + \sin(\frac{\pi}{20}))Q_1 + (\cos(\frac{3\pi}{20}) + \sin(\frac{3\pi}{20}))Q_3 = 0.
Substituting Q1=12−sin⁡(18∘)=3−54Q_1 = \frac{1}{2} - \sin(18^\circ) = \frac{3-\sqrt{5}}{4} and Q3=12−sin⁡(54∘)=1−54Q_3 = \frac{1}{2} - \sin(54^\circ) = \frac{1-\sqrt{5}}{4}, and using cos⁡(kπ20)+sin⁡(kπ20)=2sin⁡(kπ20+π4)\cos(\frac{k\pi}{20}) + \sin(\frac{k\pi}{20}) = \sqrt{2}\sin(\frac{k\pi}{20} + \frac{\pi}{4}), the equation becomes:
2sin⁡(54∘)Q1+2sin⁡(72∘)Q3=0\sqrt{2}\sin(54^\circ)Q_1 + \sqrt{2}\sin(72^\circ)Q_3 = 0.
sin⁡(54∘)(3−54)+sin⁡(72∘)(1−54)=0\sin(54^\circ)\left(\frac{3-\sqrt{5}}{4}\right) + \sin(72^\circ)\left(\frac{1-\sqrt{5}}{4}\right) = 0.
Using exact values and simplifying, this leads to 2(5−1)−10+25(5−1)=02(\sqrt{5}-1) - \sqrt{10+2\sqrt{5}}(\sqrt{5}-1) = 0, which implies 2=10+252 = \sqrt{10+2\sqrt{5}}, or 4=10+254 = 10+2\sqrt{5}, which is false. So (A) is incorrect.

(B) a1+a3+a21+a23=0a_1 + a_3 + a_{21} + a_{23} = 0
(P1+P21)Q1+(P3+P23)Q3=0(P_1 + P_{21})Q_1 + (P_3 + P_{23})Q_3 = 0
2Q1+2Q3=0  ⟹  Q1+Q3=02Q_1 + 2Q_3 = 0 \implies Q_1 + Q_3 = 0.
Q1+Q3=(12−sin⁡(π10))+(12−sin⁡(3π10))=1−(sin⁡(18∘)+sin⁡(54∘))Q_1 + Q_3 = \left(\frac{1}{2} - \sin\left(\frac{\pi}{10}\right)\right) + \left(\frac{1}{2} - \sin\left(\frac{3\pi}{10}\right)\right) = 1 - \left(\sin(18^\circ) + \sin(54^\circ)\right).
We know sin⁡(18∘)=5−14\sin(18^\circ) = \frac{\sqrt{5}-1}{4} and sin⁡(54∘)=5+14\sin(54^\circ) = \frac{\sqrt{5}+1}{4}.
So, sin⁡(18∘)+sin⁡(54∘)=5−14+5+14=254=52\sin(18^\circ) + \sin(54^\circ) = \frac{\sqrt{5}-1}{4} + \frac{\sqrt{5}+1}{4} = \frac{2\sqrt{5}}{4} = \frac{\sqrt{5}}{2}.
Thus, Q1+Q3=1−52≠0Q_1 + Q_3 = 1 - \frac{\sqrt{5}}{2} \neq 0. So (B) is incorrect.

(C) a1a3=a21a23a_1 a_3 = a_{21} a_{23}
(P1Q1)(P3Q3)=(P21Q1)(P23Q3)(P_1 Q_1)(P_3 Q_3) = (P_{21} Q_1)(P_{23} Q_3).
Since Q1≠0Q_1 \neq 0 and Q3≠0Q_3 \neq 0, we can divide by Q1Q3Q_1 Q_3, giving P1P3=P21P23P_1 P_3 = P_{21} P_{23}.
Let A=cos⁡(π20)+sin⁡(π20)A = \cos(\frac{\pi}{20}) + \sin(\frac{\pi}{20}) and B=cos⁡(3π20)+sin⁡(3π20)B = \cos(\frac{3\pi}{20}) + \sin(\frac{3\pi}{20}).
Then (1+A)(1+B)=(1−A)(1−B)(1+A)(1+B) = (1-A)(1-B), which simplifies to 1+A+B+AB=1−A−B+AB1+A+B+AB = 1-A-B+AB, so 2(A+B)=0  ⟹  A+B=02(A+B)=0 \implies A+B=0.
A+B=(cos⁡(π20)+sin⁡(π20))+(cos⁡(3π20)+sin⁡(3π20))A+B = (\cos(\frac{\pi}{20}) + \sin(\frac{\pi}{20})) + (\cos(\frac{3\pi}{20}) + \sin(\frac{3\pi}{20})).
Since π20\frac{\pi}{20} and 3π20\frac{3\pi}{20} are in the first quadrant, all terms are positive, so their sum cannot be zero. So (C) is incorrect.

(D) a1a3a21a23=1256a_1 a_3 a_{21} a_{23} = \frac{1}{256}
a1a3a21a23=(P1Q1)(P3Q3)(P21Q1)(P23Q3)=(P1P21)(P3P23)(Q1Q3)2a_1 a_3 a_{21} a_{23} = (P_1 Q_1)(P_3 Q_3)(P_{21} Q_1)(P_{23} Q_3) = (P_1 P_{21})(P_3 P_{23})(Q_1 Q_3)^2.
We found P1P21=−sin⁡(π10)P_1 P_{21} = -\sin(\frac{\pi}{10}) and P3P23=−sin⁡(3π10)P_3 P_{23} = -\sin(\frac{3\pi}{10}).
So, a1a3a21a23=(−sin⁡(π10))(−sin⁡(3π10))(Q1Q3)2=sin⁡(π10)sin⁡(3π10)(Q1Q3)2a_1 a_3 a_{21} a_{23} = (-\sin(\frac{\pi}{10}))(-\sin(\frac{3\pi}{10}))(Q_1 Q_3)^2 = \sin(\frac{\pi}{10})\sin(\frac{3\pi}{10})(Q_1 Q_3)^2.
sin⁡(π10)sin⁡(3π10)=(5−14)(5+14)=5−116=416=14\sin(\frac{\pi}{10})\sin(\frac{3\pi}{10}) = \left(\frac{\sqrt{5}-1}{4}\right)\left(\frac{\sqrt{5}+1}{4}\right) = \frac{5-1}{16} = \frac{4}{16} = \frac{1}{4}.
Q1Q3=(12−sin⁡(π10))(12−sin⁡(3π10))=14−12(sin⁡(π10)+sin⁡(3π10))+sin⁡(π10)sin⁡(3π10)Q_1 Q_3 = \left(\frac{1}{2} - \sin\left(\frac{\pi}{10}\right)\right)\left(\frac{1}{2} - \sin\left(\frac{3\pi}{10}\right)\right) = \frac{1}{4} - \frac{1}{2}(\sin(\frac{\pi}{10}) + \sin(\frac{3\pi}{10})) + \sin(\frac{\pi}{10})\sin(\frac{3\pi}{10})
=14−12(52)+14=14−54+14=2−54= \frac{1}{4} - \frac{1}{2}\left(\frac{\sqrt{5}}{2}\right) + \frac{1}{4} = \frac{1}{4} - \frac{\sqrt{5}}{4} + \frac{1}{4} = \frac{2-\sqrt{5}}{4}.
Therefore, a1a3a21a23=14(2−54)2=14(2−5)216=144−45+516=149−4516=9−4564a_1 a_3 a_{21} a_{23} = \frac{1}{4} \left(\frac{2-\sqrt{5}}{4}\right)^2 = \frac{1}{4} \frac{(2-\sqrt{5})^2}{16} = \frac{1}{4} \frac{4 - 4\sqrt{5} + 5}{16} = \frac{1}{4} \frac{9 - 4\sqrt{5}}{16} = \frac{9 - 4\sqrt{5}}{64}.
This is not equal to 1256\frac{1}{256}. So (D) is incorrect.

Based on the rigorous mathematical analysis, none of the provided options are correct.