Question

If $a_1x_1 + a_2x_2 + a_3x_3 + a_4x_4 = 1432$

$a_7x_1 + a_6x_2 + a_5x_3 + a_8x_4 = 2341$

$a_{11}x_1 + a_{12}x_2 + a_{13}x_3 + a_{10}x_4 = 3412$

$a_{17}x_1 + a_{16}x_2 + a_{15}x_3 + a_{14}x_4 = 4321$

where $a_1, a_2, a_3 ........ a_{17}$ are in A.P. with $a_1 + a_2 + a_3 ........ a_{17} = 4369$.

Then the value of $[x_1 + x_2 + x_3 + x_4]$ is (where [.] denotes G.I.F.)

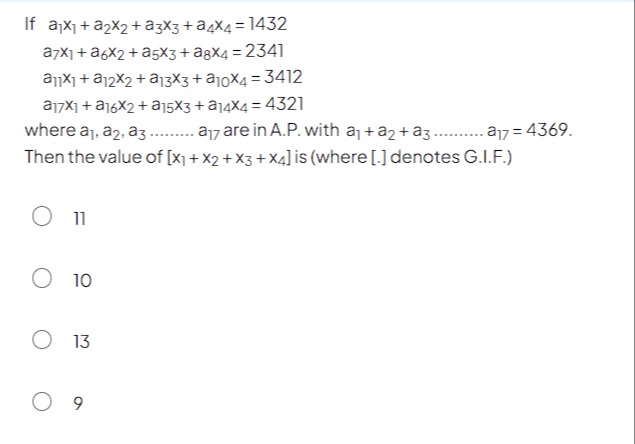
• A. 11
• B. 10
• C. 13
• D. 9

Answer 1

Answer: (A)

11

Answer 2

Let the given system of equations be:

1. $a_1x_1 + a_2x_2 + a_3x_3 + a_4x_4 = 1432$

2. $a_7x_1 + a_6x_2 + a_5x_3 + a_8x_4 = 2341$

3. $a_{11}x_1 + a_{12}x_2 + a_{13}x_3 + a_{10}x_4 = 3412$

4. $a_{17}x_1 + a_{16}x_2 + a_{15}x_3 + a_{14}x_4 = 4321$

The terms $a_1, a_2, \dots, a_{17}$ are in an arithmetic progression (A.P.). Let the first term be $A$ and the common difference be $D$. Then $a_n = A + (n-1)D$.

The sum of the first 17 terms is given as $S_{17} = a_1 + a_2 + \dots + a_{17} = 4369$.

The sum of an A.P. is $S_n = \frac{n}{2}(a_1 + a_n)$.

For $n=17$, $S_{17} = \frac{17}{2}(a_1 + a_{17}) = 4369$.

$a_1 = A$, $a_{17} = A + 16D$.

$S_{17} = \frac{17}{2}(A + A + 16D) = \frac{17}{2}(2A + 16D) = 17(A + 8D)$.

We have $17(A + 8D) = 4369$.

$A + 8D = \frac{4369}{17} = 257$.

Note that $a_9 = A + (9-1)D = A + 8D$, so $a_9 = 257$.

We want to find the value of $[x_1 + x_2 + x_3 + x_4]$. Let $S = x_1 + x_2 + x_3 + x_4$.

Let's sum the four given equations:

$(a_1x_1 + a_2x_2 + a_3x_3 + a_4x_4) + (a_7x_1 + a_6x_2 + a_5x_3 + a_8x_4) + (a_{11}x_1 + a_{12}x_2 + a_{13}x_3 + a_{10}x_4) + (a_{17}x_1 + a_{16}x_2 + a_{15}x_3 + a_{14}x_4) = 1432 + 2341 + 3412 + 4321$.

Sum of the right-hand sides: $1432 + 2341 + 3412 + 4321 = 11506$.

Rearranging the terms on the left-hand side based on $x_i$:

$(a_1 + a_7 + a_{11} + a_{17})x_1 + (a_2 + a_6 + a_{12} + a_{16})x_2 + (a_3 + a_5 + a_{13} + a_{15})x_3 + (a_4 + a_8 + a_{10} + a_{14})x_4 = 11506$.

Let's evaluate the sum of coefficients for each $x_i$:

Coefficient of $x_1$: $C_1 = a_1 + a_7 + a_{11} + a_{17}$

$C_1 = (A) + (A+6D) + (A+10D) + (A+16D) = 4A + (0+6+10+16)D = 4A + 32D = 4(A + 8D)$.

Since $A + 8D = 257$, $C_1 = 4 \times 257 = 1028$.

Coefficient of $x_2$: $C_2 = a_2 + a_6 + a_{12} + a_{16}$

$C_2 = (A+D) + (A+5D) + (A+11D) + (A+15D) = 4A + (1+5+11+15)D = 4A + 32D = 4(A + 8D)$.

$C_2 = 4 \times 257 = 1028$.

Coefficient of $x_3$: $C_3 = a_3 + a_5 + a_{13} + a_{15}$

$C_3 = (A+2D) + (A+4D) + (A+12D) + (A+14D) = 4A + (2+4+12+14)D = 4A + 32D = 4(A + 8D)$.

$C_3 = 4 \times 257 = 1028$.

Coefficient of $x_4$: $C_4 = a_4 + a_8 + a_{10} + a_{14}$

$C_4 = (A+3D) + (A+7D) + (A+9D) + (A+13D) = 4A + (3+7+9+13)D = 4A + 32D = 4(A + 8D)$.

$C_4 = 4 \times 257 = 1028$.

The sum equation becomes:

$1028x_1 + 1028x_2 + 1028x_3 + 1028x_4 = 11506$.

$1028(x_1 + x_2 + x_3 + x_4) = 11506$.

$x_1 + x_2 + x_3 + x_4 = \frac{11506}{1028}$.

Now, we perform the division:

$\frac{11506}{1028} = \frac{5753}{514}$.

Let's divide 5753 by 514:

$5753 = 5140 + 613 = 514 \times 10 + 613$.

So, $\frac{5753}{514} = 10 + \frac{613}{514}$.

The fraction $\frac{613}{514}$ is greater than 1.

$\frac{613}{514} = \frac{514 + 99}{514} = 1 + \frac{99}{514}$.

So, $x_1 + x_2 + x_3 + x_4 = 10 + 1 + \frac{99}{514} = 11 + \frac{99}{514}$.

We need to find the value of $[x_1 + x_2 + x_3 + x_4]$.

$[x_1 + x_2 + x_3 + x_4] = [11 + \frac{99}{514}]$.

Since $0 < \frac{99}{514} < 1$, the greatest integer less than or equal to $11 + \frac{99}{514}$ is 11.

The value of $[x_1 + x_2 + x_3 + x_4]$ is 11.