Question
Question: If $a_1, a_2, a_3, \dots, a_{12}$ are in A.P. and $\Delta_1 = \begin{vmatrix} a_1 a_5 & a_1 & a_2 \...
If a1,a2,a3,…,a12 are in A.P. and
Δ1=a1a5a2a6a3a7a1a2a3a2a3a4,Δ2=a2a10a3a11a4a12a2a3a4a3a4a5
then Δ1:Δ2 is equal to __
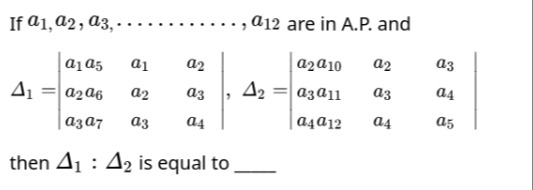
1:1
Solution
The elements a1,a2,a3,…,a12 are in A.P. Let the common difference be d. Thus, an+1−an=d for any n.
Let's analyze the determinant Δ1: Δ1=a1a5a2a6a3a7a1a2a3a2a3a4
Perform row operations to simplify the determinant:
- R2→R2−R1
- R3→R3−R2
The new determinant is: Δ1=a1a5a2a6−a1a5a3a7−a2a6a1a2−a1a3−a2a2a3−a2a4−a3
Since an are in A.P., we have a2−a1=d, a3−a2=d, a4−a3=d. Δ1=a1a5a2a6−a1a5a3a7−a2a6a1dda2dd
Now, perform another row operation: 3. R3→R3−R2
Δ1=a1a5a2a6−a1a5(a3a7−a2a6)−(a2a6−a1a5)a1d0a2d0
Let X=(a3a7−a2a6)−(a2a6−a1a5). The determinant simplifies to: Δ1=Xa1da2d Δ1=X(a1d−a2d)=Xd(a1−a2)=Xd(−d)=−Xd2
Now we need to calculate X. X=a3a7−2a2a6+a1a5. Let an=a+(n−1)d, where a is the first term. a1=a a2=a+d a3=a+2d a5=a+4d a6=a+5d a7=a+6d
Substitute these into the expression for X: X=(a+2d)(a+6d)−2(a+d)(a+5d)+a(a+4d) X=(a2+8ad+12d2)−2(a2+6ad+5d2)+(a2+4ad) X=a2+8ad+12d2−2a2−12ad−10d2+a2+4ad
Combine like terms: X=(1−2+1)a2+(8−12+4)ad+(12−10)d2 X=0a2+0ad+2d2 X=2d2.
So, Δ1=−(2d2)d2=−2d4.
Now, let's analyze Δ2: Δ2=a2a10a3a11a4a12a2a3a4a3a4a5
This determinant has the same structure as Δ1. The indices are just shifted. Applying the same row operations as for Δ1:
- R2→R2−R1
- R3→R3−R2
Δ2=a2a10a3a11−a2a10a4a12−a3a11a2dda3dd
Now, perform R3→R3−R2: Δ2=a2a10a3a11−a2a10(a4a12−a3a11)−(a3a11−a2a10)a2d0a3d0
Let Y=(a4a12−a3a11)−(a3a11−a2a10). The determinant simplifies to: Δ2=Ya2da3d Δ2=Y(a2d−a3d)=Yd(a2−a3)=Yd(−d)=−Yd2
Now we need to calculate Y. Y=a4a12−2a3a11+a2a10. Substitute an=a+(n−1)d: a2=a+d a3=a+2d a4=a+3d a10=a+9d a11=a+10d a12=a+11d
Substitute these into the expression for Y: Y=(a+3d)(a+11d)−2(a+2d)(a+10d)+(a+d)(a+9d) Y=(a2+14ad+33d2)−2(a2+12ad+20d2)+(a2+10ad+9d2) Y=a2+14ad+33d2−2a2−24ad−40d2+a2+10ad+9d2
Combine like terms: Y=(1−2+1)a2+(14−24+10)ad+(33−40+9)d2 Y=0a2+0ad+2d2 Y=2d2.
So, Δ2=−(2d2)d2=−2d4.
Finally, we need to find the ratio Δ1:Δ2: Δ1:Δ2=(−2d4):(−2d4)=1:1
The final answer is 1:1.
Explanation of the solution:
- Simplify Determinants using Row Operations: Both determinants Δ1 and Δ2 have a similar structure. By applying row operations R2→R2−R1 and then R3→R3−R2, two elements in the third row become zero. This reduces the determinant to a product of one element from the first column of the modified matrix and a 2×2 minor.
- Utilize A.P. Properties: The differences an+1−an=d are used directly in the row operations, simplifying the second and third columns. The 2×2 minor that results is of the form aidai+1d, which evaluates to d(ai−ai+1)=d(−d)=−d2.
- Calculate the Remaining Term: The non-zero element in the third row of the modified determinant is a second-order difference of terms like anan+k. For Δ1, this term is X=a3a7−2a2a6+a1a5. For Δ2, it is Y=a4a12−2a3a11+a2a10.
- Evaluate Second Differences: Since an is an A.P., an=a+(n−1)d. A product of two terms from an A.P., like anan+k, is a quadratic function of n. The second difference of a quadratic Pn2+Qn+R is 2P. In our case, the coefficient of n2 in anan+k is d2. Thus, both X and Y evaluate to 2d2.
- Calculate Determinants: Both Δ1 and Δ2 simplify to −(2d2)d2=−2d4.
- Find the Ratio: The ratio Δ1:Δ2 is therefore (−2d4):(−2d4)=1:1.
