Question
Question: If $A = \{x \in \mathbb{R} \mid \sin^{-1}(\sqrt{x^2+x+1}) \in [-\frac{\pi}{2}, \frac{\pi}{2}]\}$ and...
If A={x∈R∣sin−1(x2+x+1)∈[−2π,2π]} and B={y∈R∣y=sin−1(x2+x+1),x∈A}, then
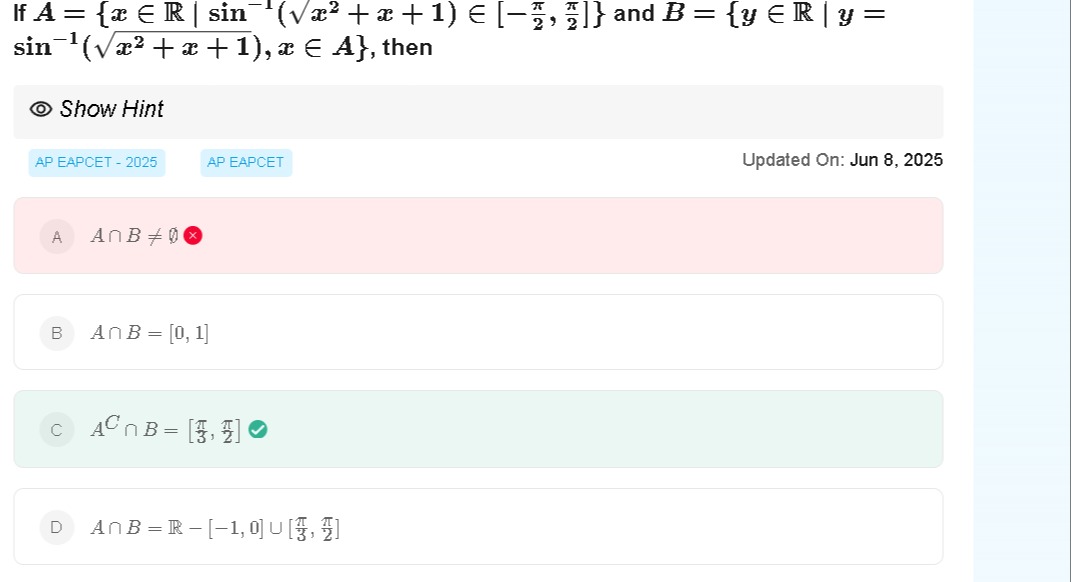
A∩B=∅
A∩B=[0,1]
AC∩B=[3π,2π]
A∩B=R−[−1,0]∪[3π,2π]
C
Solution
Step-by-step Derivations:
1. Determine Set A:
Set A is defined as A={x∈R∣sin−1(x2+x+1)∈[−2π,2π]}.
For sin−1(z) to be defined, its argument z must satisfy −1≤z≤1. Here, z=x2+x+1. So, we need: a. x2+x+1≥0 b. x2+x+1≤1
Let's analyze the quadratic expression x2+x+1. The discriminant is Δ=b2−4ac=(1)2−4(1)(1)=1−4=−3. Since Δ<0 and the leading coefficient (1) is positive, the quadratic x2+x+1 is always positive for all x∈R. Therefore, x2+x+1 is always defined and positive, satisfying condition (a).
Now consider condition (b): x2+x+1≤1. Since both sides are non-negative, we can square both sides without changing the inequality direction: x2+x+1≤12 x2+x+1≤1 x2+x≤0 Factor out x: x(x+1)≤0 This inequality holds when x and (x+1) have opposite signs or one of them is zero. The roots are x=0 and x=−1. The expression x(x+1) is a parabola opening upwards, so it is less than or equal to zero between its roots. Thus, −1≤x≤0.
The range of sin−1(z) is inherently [−2π,2π]. So, if sin−1(x2+x+1) is defined, it will automatically fall within this range. Therefore, set A is the set of all x for which the expression is defined: A=[−1,0].
2. Determine Set B:
Set B is defined as B={y∈R∣y=sin−1(x2+x+1),x∈A}. This means B is the range of the function f(x)=sin−1(x2+x+1) for x∈[−1,0].
Let's find the range of the inner function u(x)=x2+x+1 for x∈[−1,0]. This is a parabola opening upwards. Its vertex is at x=−2ab=−2(1)1=−21. Since x=−1/2 is within the interval [−1,0], the minimum value of u(x) occurs at the vertex: umin=u(−1/2)=(−1/2)2+(−1/2)+1=1/4−1/2+1=1/4−2/4+4/4=3/4.
The maximum value of u(x) in the interval [−1,0] occurs at one of the endpoints: u(−1)=(−1)2+(−1)+1=1−1+1=1. u(0)=(0)2+(0)+1=1. So, for x∈[−1,0], the range of u(x)=x2+x+1 is [3/4,1].
Next, consider the function g(u)=u. This function is increasing. So, for u∈[3/4,1], the range of u is [3/4,1]=[23,1].
Finally, consider the function h(v)=sin−1(v). This function is also increasing. So, for v∈[23,1], the range of sin−1(v) is [sin−1(23),sin−1(1)]. We know that sin(3π)=23 and sin(2π)=1. Therefore, sin−1(23)=3π and sin−1(1)=2π. So, set B is [3π,2π].
3. Evaluate the Options:
We have A=[−1,0] and B=[3π,2π]. Note that 3π≈1.047 and 2π≈1.571.
A. A∩B=∅
A=[−1,0] (contains non-positive numbers). B=[3π,2π] (contains positive numbers greater than 1). The intervals are disjoint. A∩B=∅. So, option A is incorrect.
B. A∩B=[0,1]
As determined above, A∩B=∅. So, option B is incorrect.
C. AC∩B=[3π,2π]
First, find AC (complement of A in R): AC=R∖[−1,0]=(−∞,−1)∪(0,∞). Now, find AC∩B: AC∩B=((−∞,−1)∪(0,∞))∩[3π,2π]. Since 3π>0, the entire interval B=[3π,2π] lies within the interval (0,∞). Therefore, AC∩B=[3π,2π]. So, option C is correct.
D. A∩B=R−[−1,0]∪[3π,2π]
We know A∩B=∅. The set R−[−1,0]∪[3π,2π] is not empty. So, option D is incorrect.
