Question

If a wire is stretched to n times of its original length, its new resistance will be
(A) $\dfrac{1}{n}$ times
(B) ${n^2}$ times
(C) n times
(D) None

Answer 1

Hint The resistance of the conductor is given by $R = \rho \dfrac{l}{A}$ ; it is directly proportional to length and inversely proportional to area. When length is extended by some measure the area gets reduced by the same measure. Substitute length and area after extension again to get the new resistance.

Complete step-by-step solution
Resistance of a substance is a property by virtue of which it opposes the flow of current through it. This resistance of the conductor is given by
$R = \rho \dfrac{l}{A}$
Where, l is the length of the conductor, A is the area of cross section and ρ is the resistivity of the material.

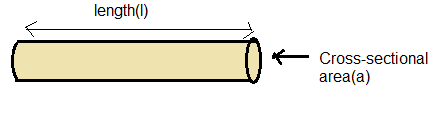
From the above expression we know that
$R \propto l \\\ R \propto \dfrac{1}{A} \\\$
When the conductor’s length is increased by n times by stretching the area becomes n times less, so
Let l’ and A’ be the length and area after stretching
l’=nl
$A' = \dfrac{A}{n}$
Substitute the new length and area,
$R' = \rho \dfrac{{nl}}{{\left( {\dfrac{A}{n}} \right)}} \\\ R' = {n^2}\rho \dfrac{l}{A} \\\ R' = {n^2}R \\\$

Hence, the new resistance is ${n^2}$ the resistance before and the correct option is B.

Note The resistance is directly proportional to temperature so, resistance increases when temperature is more and vice versa. If ${R_1}$ and ${R_2}$ are resistance at temperature ${T_1}$ and ${T_2}$
$\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{1 + \alpha {T_1}}}{{1 + \alpha {T_2}}}$
$\propto$ are the temperature coefficients.