Question

If a vector $\overrightarrow{A}$ makes angles $\alpha,\beta$ and $\gamma$ with $X$,$Y$ and $Z$ axes respectively then $sin^{2}\alpha+sin^{2}\beta+sin^{2}\gamma=$

& A.0 \\\ & B.1 \\\ & C.2 \\\ & D.3 \\\ \end{aligned}$$

Answer 1

We know that a vector has both length or magnitude and direction. The angle the vector makes with the axis give the direction or the orientation of the vector on any given space. Generally, a vector is said to make $\alpha,\beta$ and $\gamma$ with $X$,$Y$ and $Z$ axes respectively.

Complete step by step answer:
Given that the vector $\overrightarrow{A}$ makes angles $\alpha,\beta$ and $\gamma$with $X$,$Y$ and $Z$ axes respectively. This implies that the unit vector $\hat{a}$, also known as the directional vector is as shown in the figure. Then we can express the vector $\overrightarrow{A}$ as $\vec A=a_{x}\hat i+a_{y}\hat j+a_{z}\hat k$, and the unit vector $\hat{a}$ is given as, $\hat a=\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}$

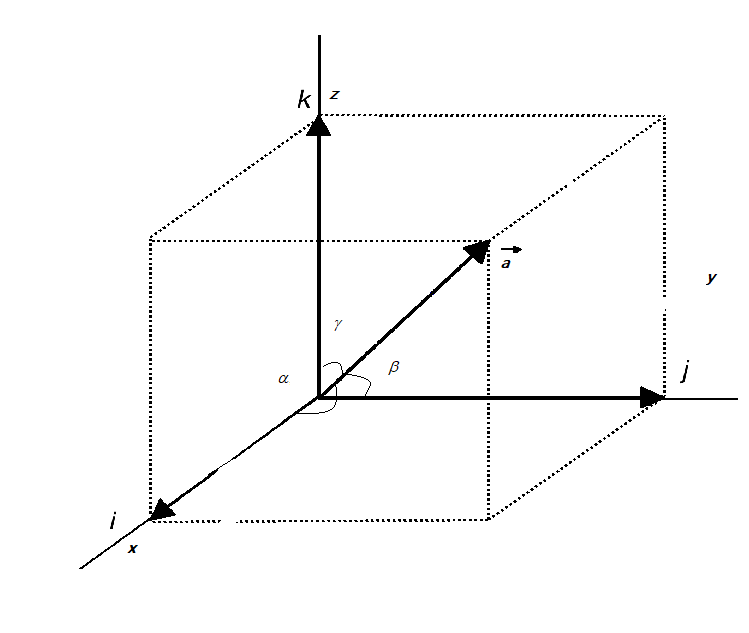
We can then express, the x,y,z components of the vectors with respect to the angles as the following:
$cos\alpha=\dfrac{a_{x}\hat i}{\hat a}$
$cos\beta=\dfrac{a_{y}\hat j}{\hat a}$
$cos\gamma=\dfrac{a_{z}\hat k}{\hat a}$
Squaring and adding, we get, $cos^{2}\alpha+cos^{2}\beta+cos^{2}\gamma=\dfrac{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}{\left(\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}\right)^{2}}=1$
Thus, $cos^{2}\alpha+cos^{2}\beta+cos^{2}\gamma=1$
But we need $sin^{2}\alpha+sin^{2}\beta+sin^{2}\gamma$
We know from trigonometry identities, that $sin^{2}\theta+cos^{2}\theta=1$
Then, we can write, $cos^{2}\alpha+cos^{2}\beta+cos^{2}\gamma=1-sin^{2}\alpha+1-sin^{2}\beta+1-sin^{2}\gamma=3-(sin^{2}\alpha+sin^{2}\beta+sin^{2}\gamma)$
Then,$3-(sin^{2}\alpha+sin^{2}\beta+sin^{2}\gamma)=1$
Or,$sin^{2}\alpha+sin^{2}\beta+sin^{2}\gamma=3-1=2$
Thus, $sin^{2}\alpha+sin^{2}\beta+sin^{2}\gamma=2$
Hence C.$2$ is the answer.

Additional information:
We know that two vectors can be added, subtracted, and multiplied. We also know that the algebraic laws such as commutativity, associativity and distributivity are valid to certain degree and not always applicable. If a scalar and a vector is multiplied, it is said to be scalar multiplication or dot product. If a vector and another vector are multiplied, then it is said to be cross product or vector multiplication.

Note: When we say a $\vec{AB}$, we mean that $A$ is carried to $B$ in a particular direction in the space. Also magnitude denoted as $|\vec{AB}|$ gives the distance between the points $A$ and $B$. these vectors are generally represented on the coordinate systems.