Question
Question: If a variable takes the discrete values $$\alpha - 4, \alpha - \frac{7}{2}, \alpha - 3, \alpha - \fr...
If a variable takes the discrete values α−4,α−27,α−3,α−25,α−2,α−21,α+21,α+5(α>0), then its median is
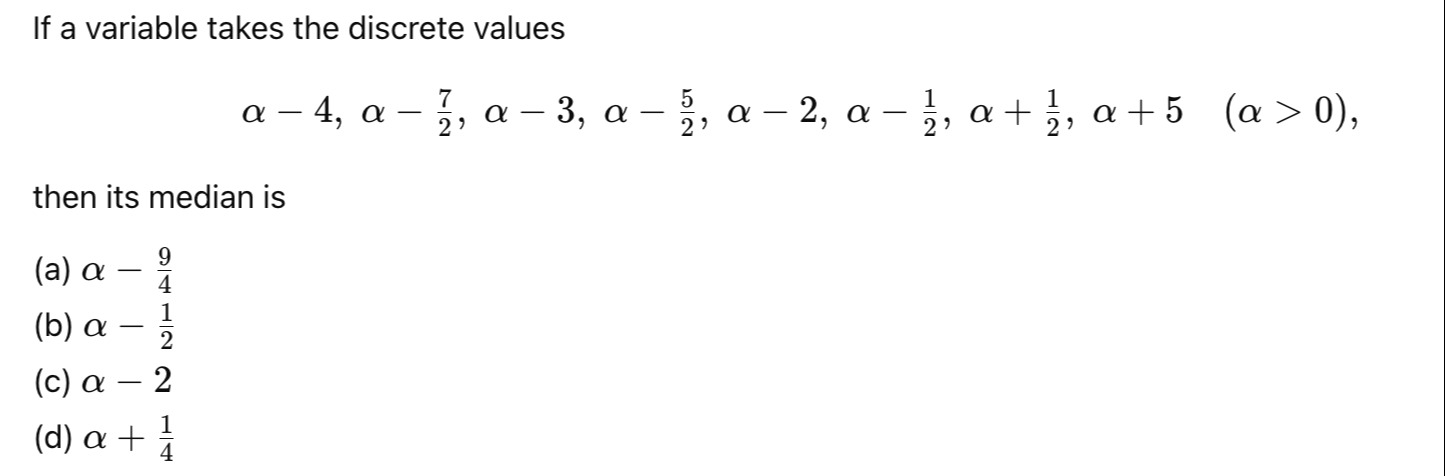
α−49
α−21
α−2
α+41
α−49
Solution
To find the median of the given discrete values, we first need to arrange them in ascending order. The given values are: α−4,α−27,α−3,α−25,α−2,α−21,α+21,α+5 There are 8 values. We can determine the order by comparing the constant terms: −4,−27,−3,−25,−2,−21,21,5 Converting these to decimals for easier comparison: −4.0,−3.5,−3.0,−2.5,−2.0,−0.5,0.5,5.0 Arranging these constants in ascending order gives: −4.0,−3.5,−3.0,−2.5,−2.0,−0.5,0.5,5.0 So, the values arranged in ascending order are: α−4,α−27,α−3,α−25,α−2,α−21,α+21,α+5 The number of values is n=8, which is an even number. For an even number of data points, the median is the average of the 2n-th and (2n+1)-th values in the sorted list. Here, n=8, so 2n=28=4. The median is the average of the 4th and 5th values.
From the sorted list: The 4th value is α−25. The 5th value is α−2.
The median is the average of these two values: Median=2(α−25)+(α−2) Median=2α−2.5+α−2 Median=22α−4.5 Median=22α−29 Median=22α−229 Median=α−49
Comparing this result with the given options, the calculated median α−49 matches option (a).
