Solveeit Logo
Login

Question

Question: If a trigonometric equation is given as \(1+{{\sin }^{2}}\theta =3\sin \theta \cos \theta \) , then ...

If a trigonometric equation is given as 1+sin⁡2θ=3sin⁡θcos⁡θ1+{{\sin }^{2}}\theta =3\sin \theta \cos \theta , then prove that tan⁡θ=1 or 12\tan \theta =1\text{ or }\dfrac{1}{2} .

Explanation

Solution

Hint: Try to simplify the equation given in the question to reach a quadratic equation in terms of tan⁡θ\tan \theta . Solve the quadratic equation using the quadratic formula to reach the required result.

Complete step-by-step solution -
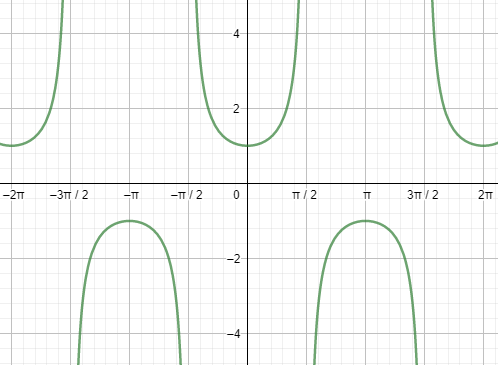
Before moving to the solution, let us discuss the periodicity of the secant and tangent function, which we would be using in the solution. All the trigonometric ratios, including secant and tangent, are periodic functions. We can better understand this using the graph of secant and tangent.
First, let us start with the graph of secx.

Next, let us see the graph of tanx.

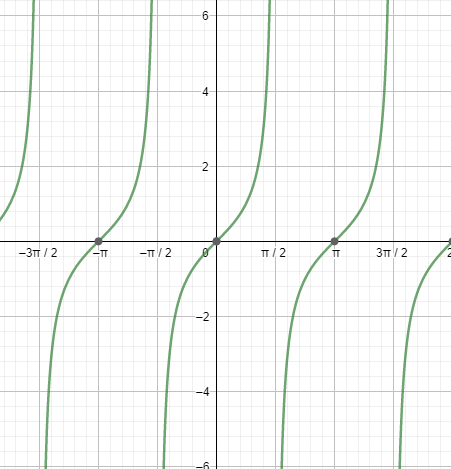
Looking at both the graphs, we can say that the graphs are repeating after a fixed period i.e. 2πc2{{\pi }^{c}} . So, we can say that the fundamental period of the secant function and the tangent function is 2πc=360∘2{{\pi }^{c}}=360{}^\circ
We will now simplify the equation given in the question.
1+sin⁡2θ=3sin⁡θcos⁡θ1+{{\sin }^{2}}\theta =3\sin \theta \cos \theta
Now we will divide both the sides of the equation by cos⁡2θ{{\cos }^{2}}\theta . Therefore, our equation becomes:
1cos⁡2θ+sin⁡2θcos⁡2θ=3sin⁡θcos⁡θcos⁡2θ\dfrac{1}{{{\cos }^{2}}\theta }+\dfrac{{{\sin }^{2}}\theta }{{{\cos }^{2}}\theta }=\dfrac{3\sin \theta \cos \theta }{{{\cos }^{2}}\theta }

As we know that 1cos⁡θ=sec⁡θ\dfrac{1}{\cos \theta }=\sec \theta and sin⁡θcos⁡θ=tan⁡θ\dfrac{\sin \theta }{\cos \theta }=\tan \theta , we can say that:
sec⁡2θ+tan⁡2θ=3tan⁡θ{{\sec }^{2}}\theta +{{\tan }^{2}}\theta =3\tan \theta
Now, if we use the formula sec⁡2θ=1+tan⁡2θ{{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta , we get
1+tan⁡2θ+tan⁡2θ=3tan⁡θ1+{{\tan }^{2}}\theta +{{\tan }^{2}}\theta =3\tan \theta
⇒2tan⁡2θ−3tan⁡θ+1=0\Rightarrow 2{{\tan }^{2}}\theta -3\tan \theta +1=0
Now as the above equation is a quadratic equation. So, we will use the quadratic formula to find the roots of the equation.
∴tan⁡θ=−b±b2−4ac2a=−(−3)±(−3)2−4×2×14=3±14\therefore \tan \theta =\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}=\dfrac{-\left( -3 \right)\pm \sqrt{{{\left( -3 \right)}^{2}}-4\times 2\times 1}}{4}=\dfrac{3\pm 1}{4}
Therefore, the possible values of tan⁡θ\tan \theta are 1 and 12\dfrac{1}{2} .

Note: While simplifying trigonometric equations, it is always preferred to convert the equation to a form containing the least number of different trigonometric ratios. Also, give a thought to the trigonometric ratios involved in the expression, which is asked in the question, as that might give you a hint to solve the problem.